If you are searching for instant help on the concepts of Algebra 1 Ch 5 Solving Systems of Linear Equations then this is the one-stop destination for all your needs. Make the most out of the BIM Book Algebra 1 Chapter 5 Solving Systems of Linear Equations Solutions Key provided and clarify your doubts on the same. You need not worry about the accuracy of the Solving Systems of Linear Equations Big Ideas Math Algebra 1 Answers Chapter 5 as they are given to you by subject experts.
To make it easy for you we have compiled the Big Ideas Math Algebra 1 Answers for Chapter 5 Textbook Questions via quick links available here. You can tap on them or download them free of cost and prepare effectively. Practice the BIM Textbook Algebra 1 Ch 5 Solving Systems of Linear Equations Answers on a regular basis so that your speed and accuracy will be improved in the actual exams.
Big Ideas Math Book Algebra 1 Answer Key Chapter 5 Solving Systems of Linear Equations
We have covered all the Questions from Exercises(5.1 to 5.7), Chapter Tests, Review Tests, Quiz, Assessment Tests, Cumulative Assessments, etc. in the Solving Systems of Linear Equations Big Ideas Math Algebra 1 Answer Key. You can understand the topics in it easily as they are explained in an elaborate manner keeping in mind your level of understanding.
- Solving Systems of Linear Equations Maintaining Mathematical Proficiency – Page 233
- Solving Systems of Linear Equations Mathematical Practices – Page 234
- Lesson 5.1 Solving Systems of Linear Equations by Graphing – Page(235-240)
- Solving Systems of Linear Equations by Graphing 5.1 Exercises – Page(239-240)
- Lesson 5.2 Solving Systems of Linear Equations by Substitution – Page(241-246)
- Solving Systems of Linear Equations by Substitution 5.2 Exercises – Page(245-246)
- Lesson 5.3 Solving Systems of Linear Equations by Elimination – Page(247-252)
- Solving Systems of Linear Equations by Elimination 5.3 Exercises – Page(251-252)
- Lesson 5.4 Solving Special Systems of Linear Equations – Page(253-258)
- Solving Special Systems of Linear Equations 5.4 Exercises – Page(257-258)
- Solving Systems of Linear Equations Study Skills: Analyzing Your Errors – Page 259
- Solving Systems of Linear Equations 5.1–5.4 Quiz – Page 260
- Lesson 5.5 Solving Equations by Graphing – Page(261-266)
- Solving Equations by Graphing 5.5 Exercises – Page(265-266)
- Lesson 5.6 Graphing Linear Inequalities in Two Variables – Page(267-272)
- Graphing Linear Inequalities in Two Variables 5.6 Exercises – Page(271-272)
- Lesson 5.7 Systems of Linear Inequalities – Page(273-280)
- Systems of Linear Inequalities 5.7 Exercises – Page(278-280)
- Solving Systems of Linear Equations Performance Task: Prize Patrol – Page 281
- Solving Systems of Linear Equations Chapter Review – Page(282-284)
- Solving Systems of Linear Equations Chapter Test – Page 285
- Solving Systems of Linear Equations Cumulative Assessment – Page(286-287)
Solving Systems of Linear Equations Maintaining Mathematical Proficiency
Graph the equation.
Question 1.
y + 4 = x
Answer:
x – y = 4
Question 2.
6x – y = -1
Answer:
Question 3.
4x + 5y = 20
Answer:
Question 4.
-2y + 12 = -3x
Answer:
Solve the inequality. Graph the solution.
Question 5.
m + 4 > 9
Answer:
m + 4 > 9
m > 9 – 4
m > 5
Question 6.
24 ≤ -6t
Answer:
Question 7.
2a – 5 ≤ 13
Answer:
Question 8.
-5z + 1 < -14
Answer:
-5z < -14 – 1
-5z < -15
z > 3
Question 9.
4k – 16 < k + 2
Answer:
4k – 16 < k + 2
4k – k < 2 + 16
3k < 18
k < 6
Question 10.
7w + 12 ≥ 2w – 3
Answer:
7w + 12 ≥ 2w – 3
7w -2w ≥ -12 – 3
5w ≥ -15
w ≥ -3
Question 11.
ABSTRACT REASONING
The graphs of the linear functions g and h have different slopes. The value of both functions at x = a is b. When g and h are graphed in the same coordinate plane, what happens at the point (a, b)?
Answer:
Solving Systems of Linear Equations Mathematical Practices
Mathematically proficient students use technological tools to explore concepts.
Monitoring Progress
Use a graphing calculator to find the point of intersection of the graphs of the two linear equations.
Question 1.
y = -2x – 3
y = \(\frac{1}{2}\)x – 3
Answer:
Question 2.
y = -x + 1
y = x- 2
Answer:
Question 3.
3x – 2y = 2
2x – y = 2
Answer:
Lesson 5.1 Solving Systems of Linear Equations by Graphing
Essential Question How can you solve a system of linear equations?
EXPLORATION 1
Writing a System of Linear Equations Work with a partner. Your family opens a bed-and-breakfast. They spend $600 preparing a bedroom to rent. The cost to your family for food and utilities is $15 per night. They charge $75 per night to rent the bedroom.
a. Write an equation that represents the costs.
b. Write an equation that represents the revenue (income).
c. A set of two (or more) linear equations is called a system of linear equations. Write the system of linear equations for this problem.
Answer:
a. C = 15 . x + $600
C = 15x + 600
b. R = $75 . x
R = 75x
c.
C = 15x + 600
y = 15x + 600
R = 75x
y = 75x
EXPLORATION 2
Using a Table or Graph to Solve a System
Work with a partner. Use the cost and revenue equations from Exploration 1 to determine how many nights your family needs to rent the bedroom before recovering the cost of preparing the bedroom. This is the break-even point.
a. Copy and complete the table.
b. How many nights does your family need to rent the bedroom before breaking even?
c. In the same coordinate plane, graph the cost equation and the revenue equation from Exploration 1.
d. Find the point of intersection of the two graphs. What does this point represent? How does this compare to the break-even point in part (b)? Explain.
Answer:
C = 15x + 600
x = 0
C = 600
x=1
C = 15 + 600 = 615
x = 2
C = 15(2) + 600
C = 30 + 600 = 630
x = 3
C = 15(3) + 600 = 45 + 600 = 645
x = 4
C = 60 + 600 = 660
x = 5
C = 75 + 600 = 675
x = 6
C = 90 + 600 = 690
x = 7
C = 105 + 600 = 705
x = 8
C = 120 + 600 = 720
x = 9
C = 135 + 600 = 735
x = 10
C = 150 + 600 = 750
x = 11
C = 165 + 600 = 765
R = 75x
x = 0
R = 75(0) = 0
x = 1
R = 75(1) = 75
x = 2
R = 75(2) = 150
x = 3
R = 75(3) = 225
x = 4
R = 300
x = 5
R = 375
x = 6
R = 450
x = 7
R = 525
x = 8
R = 600
x = 9
R = 675
x = 10
R = 750
x = 11
R = 825
b. 11 nights
Communicate Your Answer
Question 3.
How can you solve a system of linear equations? How can you check your solution?
Answer:
Question 4.
Solve each system by using a table or sketching a graph. Explain why you chose each method. Use a graphing calculator to check each solution.
a. y = -4.3x – 1.3
y = 1.7x + 4.7
Answer:
b. y = x
y = -3x + 8
Answer:
c. y = -x – 1
y = 3x + 5
Answer:
Monitoring Progress
Tell whether the ordered pair is a solution of the system of linear equations.
Question 1.
(1, -2); 2x + y = 0
-x + 2y = 5
Answer:
2x +y = 0
2(1) + (-2) = 0
2 – 2 = 0
The solution works on the first equation.
-x + 2y = 5
-1 + 2(-2) = 5
-1 – 4 = 5
-5 = 5
The solution does not work in the second solution.
Question 2.
(1, 4); y = 3x + 1
y = -x + 5
Answer:
Given,
(1, 4); y = 3x + 1
y = -x + 5
y = 3x + 1
4 = 3(1) + 1
4 = 4
The solution works on the first equation.
y = -x + 5
4 = -1 + 5
4 = 4
The solution works on the second equation.
Solve the system of linear equations by graphing.
Question 3.
y = x – 2
y = -x + 4
Answer:
Question 4.
y = \(\frac{1}{2}\)x + 3
y = –\(\frac{3}{2}\)x – 5
Answer:
Question 5.
2x + y = 5
3x – 2y = 4
Answer:
Question 6.
You have a total of 18 math and science exercises for homework. You have six more math exercises than science exercises. How many exercises do you have in each subject?
Answer:
x + y = 18
x = 6 + y
x – y = 6
2x = 24
x = 12
Solving Systems of Linear Equations by Graphing 5.1 Exercises
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
Do the equations 5y – 2x = 18 and 6x = -4y – 10 form a system of linear equations? Explain.
Answer:
Question 2.
DIFFERENT WORDS, SAME QUESTION
Consider the system of linear equations -4x + 2y = 4 and 4x – y = -6. Which is different? Find “both” answers.
Answer:

Monitoring Progress and Modeling with Mathematics
In Exercises 3–8, tell whether the ordered pair is a solution of the system of linear equations.
Question 3.
(2, 6); x + y = 8
3x – y = 0
Answer:
Question 4.
(8, 2); x – y = 6
2x – 10y = 4
Answer:
Question 5.
(-1, 3); y = -7x – 4
y = 8x + 5
Answer:
Question 6.
(-4, -2); y = 2x + 6
y = -3x – 14
Answer:
Question 7.
(-2, 1); 6x + 5y = -7
2x – 4y = -8
Answer:
Question 8.
(5, -6); 6x + 3y = 12
4x + y = 14
Answer:
In Exercises 9–12, use the graph to solve the system of linear equations. Check your solution.
Question 9.
x – y = 4
4x + y = 1
Answer:
Question 10.
x + y = 5
y – 2x = -4
Answer:
Question 11.
6y + 3x = 18
-x + 2y = 24
Answer:
Question 12.
2x – y = -2
2x + 4y = 8
Answer:
In Exercises 13–20, solve the system of linear equations by graphing.
Question 13.
y = -x + 7
y = x + 1
Answer: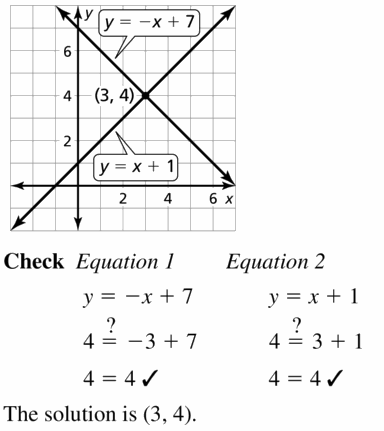
Question 14.
y = -x + 4
y = 2x – 8
Answer:
y=0
Question 15.
y = \(\frac{1}{3}\)x + 2
y = \(\frac{2}{3}\)x + 5
Answer: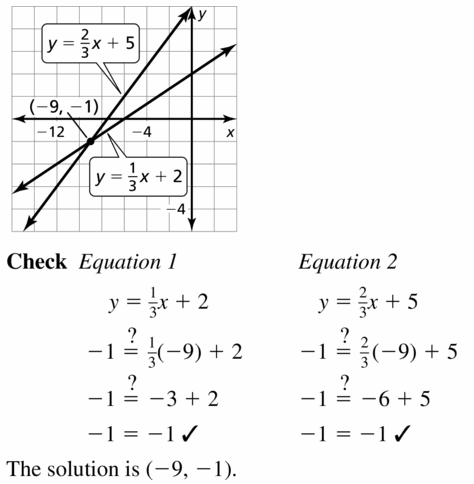
Question 16.
y = \(\frac{3}{4}\)x – 4
y = –\(\frac{1}{2}\)x + 11
Answer:


Question 17.
9x + 3y = -3
2x – y = -4
Answer:

Question 18.
4x – 4y = 20
y = -5
Answer:
Question 19.
x – 4y = -4
-3x – 4y = 12
Answer:

Question 20.
3y + 4x = 3
x + 3y = -6
Answer:
ERROR ANALYSIS In Exercises 21 and 22, describe and correct the error in solving the system of linear equations.
Question 21.
Answer:

Question 22.
Answer:
USING TOOLS In Exercises 23–26, use a graphing calculator to solve the system of linear equations.
Question 23.
0.2x + 0.4y = 4
-0.6x + 0.6y = -3
Answer:
Question 24.
-1.6x – 3.2y = -24
2.6x + 2.6y = 26
Answer:
Question 25.
-7x + 6y = 0
0.5x + y = 2
Answer:
Question 26.
4x – y = 1.5
2x + y = 1.5
Answer:
Question 27.
MODELING WITH MATHEMATICS
You have 40 minutes to exercise at the gym, and you want to burn 300 calories total using both machines. How much time should you spend on each machine?
Answer:


Question 28.
MODELING WITH MATHEMATICS
You sell small and large candles at a craft fair. You collect $144 selling a total of 28 candles. How many of each type of candle did you sell?
Answer:

Question 29.
MATHEMATICAL CONNECTIONS
Write a linear equation that represents the area and a linear equation that represents the perimeter of the rectangle. Solve the system of linear equations by graphing. Interpret your solution.
Answer:


Question 30.
THOUGHT PROVOKING
Your friend’s bank account balance (in dollars) is represented by the equation y = 25x + 250, where x is the number of months. Graph this equation. After 6 months, you want to have the same account balance as your friend. Write a linear equation that represents your account balance. Interpret the slope and y-intercept of the line that represents your account balance.
Answer:

Question 31.
COMPARING METHODS
Consider the equation x + 2 = 3x – 4.
a. Solve the equation using algebra.
b. Solve the system of linear equations y = x + 2 and y = 3x – 4 by graphing.
c. How is the linear system and the solution in part (b) related to the original equation and the solution in part (a)?
Answer:

Question 32.
HOW DO YOU SEE IT?
A teacher is purchasing binders for students. The graph shows the total costs of ordering x binders from three different companies.
a. For what numbers of binders are the costs the same at two different companies? Explain.
b. How do your answers in part (a) relate to systems of linear equations?
Answer:

Question 33.
MAKING AN ARGUMENT
You and a friend are going hiking but start at different locations. You start at the trailhead and walk 5 miles per hour. Your friend starts 3 miles from the trailhead and walks 3 miles per hour.
a. Write and graph a system of linear equations that represents this situation.
b. Your friend says that after an hour of hiking you will both be at the same location on the trail. Is your friend correct? Use the graph from part (a) to explain your answer.
Answer:

Maintaining Mathematical Proficiency
Solve the literal equation for y.
Question 34.
10x + 5y = 5x + 20
Answer:
10x + 5y = 5x + 20
10x + 5y – 5x = 20
5x + 5y = 20
x + y = 4
y = 4 – x
Question 35.
9x + 18 = 6y – 3x
Answer:
9x + 18 = 6y – 3x
9x + 3x + 18 = 6y
12x + 18 = 6y
2x + 3 = y
So, the equation is y = 2x + 3
Question 36.
\(\frac{3}{4}\) x + \(\frac{1}{4}\) y = 5
Answer:
Given equation is \(\frac{3}{4}\) x + \(\frac{1}{4}\) y = 5
\(\frac{3}{4}\) x – \(\frac{3}{4}\) x + \(\frac{1}{4}\) y = 5 – \(\frac{3}{4}\) x
\(\frac{1}{4}\) y = 5 – \(\frac{3}{4}\) x
Multiply by 4 on both sides
\(\frac{1}{4}\) y × 4 = (5 – \(\frac{3}{4}\) x)4
y = 20 – 3x
Lesson 5.2 Solving Systems of Linear Equations by Substitution
Essential Question How can you use substitution to solve a system of linear equations?
EXPLORATION 1
Using Substitution to Solve Systems
Work with a partner. Solve each system of linear equations using two methods.
Method 1 Solve for x first.
Solve for x in one of the equations. Substitute the expression for x into the other equation to find y. Then substitute the value of y into one of the original equations to find x.
Method 2 Solve for y first.
Solve for y in one of the equations. Substitute the expression for y into the other equation to find x. Then substitute the value of x into one of the original equations to find y.
Is the solution the same using both methods? Explain which method you would prefer to use for each system
a. x + y = -7
-5x + y = 5
Answer:
x + y = -7
-5x + y = 5
Solve for x
x + y = -7
-5x + y = 5
+ – –
6x = -12
x = -2
-2 + y = -7
y = -7 + 2
y = -5
b. x – 6y = -11
3x + 2y = 7
Answer:
x – 6y = -11
3x + 2y = 7— × 3
9x + 6y = 21
x – 6y = -11
9x + 6y = 21
10x = 10
x = 1
3(1) + 2y = 7
3 + 2y = 7
2y = 7 – 3
2y = 4
y = 2
So, x = 1 and y = 2
c. 4x + y = -1
3x – 5y = -18
Answer:
4x + y = -1 — × 5 ⇒ 20x + 5y = -5
3x – 5y = -18
20x + 5y = -5
3x – 5y = -18
23x = -23
x = -1
4x + y = -1
4(-1) + y = -1
-4 + y = -1
y = -1 + 4
y = 3
EXPLORATION 2
Writing and Solving a System of Equations
Work with a partner.
a. Write a random ordered pair with integer coordinates. One way to do this is to use a graphing calculator. The ordered pair generated at the right is (-2, -3).
b. Write a system of linear equations that has your ordered pair as its solution.
c. Exchange systems with your partner and use one of the methods from Exploration 1 to solve the system. Explain your choice of method.
Communicate Your Answer
Question 3.
How can you use substitution to solve a system of linear equations?
Answer:
Step 1 : First, solve one linear equation for y in terms of x .
Step 2 : Then substitute that expression for y in the other linear equation.
Step 3 : Solve this, and you have the x -coordinate of the intersection.
Step 4 : Then plug in x to either equation to find the corresponding y -coordinate.
Question 4.
Use one of the methods from Exploration 1 to solve each system of linear equations. Explain your choice of method. Check your solutions.
a. x + 2y = -7
2x – y = -9
Answer:
x + 2y = -7—– × 2 ⇒ 2x + 4y = -14
2x – y = -9
2x + 4y = -14
2x – y = -9
– + +
5y = -5
y = -1
x + 2y = -7
x + 2(-1) = -7
x – 2 = -7
x = -7 + 2
x = -5
b.x – 2y = -6
2x + y = -2
Answer:
x – 2y = -6
2x + y = -2 — × 2
x – 2y = -6
4x + 2y = -4
5x = -10
x = -2
x – 2y = -6
-2 – 2y = -6
-2y = -6 + 2
-2y = -4
y = 2
c.-3x + 2y = -10
-2x + y = -6
Answer:
-3x + 2y = -10
-2x + y = -6 —- × 2 ⇒ -4x + 2y = -12
-3x + 2y = -10
-4x + 2y = -12
+ – +
x = 2
-2x + y = -6
-2(2) + y = -6
-4 + y = -6
y = -6 + 4
y = -2
d. 3x + 2y = 13
x – 3y = -3
Answer:
3x + 2y = 13
x – 3y = -3 — × 3 ⇒ 3x – 9y = -9
3x + 2y = 13
3x – 9y = -9
– + +
11y = 22
y = 2
x – 3(2) = -3
x – 6 = -3
x = -3 + 6
x = 3
e. 3x – 2y = 9
-x – 3y = 8
Answer:
3x – 2y = 9
-x – 3y = 8 —- × 3 ⇒ -3x – 9y = 24
3x – 2y = 9
-3x – 9y = 24
-11y = 33
y = -3
-x – 3(-3) = 8
-x + 9 = 8
-x = -1
x = 1
f. 3x – y = -6
4x + 5y = 11
Answer:
3x – y = -6 —– × 5 ⇒ 15x – 5y = -30
4x + 5y = 11
15x – 5y = -30
4x + 5y = 11
19x = -19
x = -1
3x – y = -6
3(-1) – y = -6
-3 – y = -6
-y = -6 + 3
-y = -3
y = 3
Monitoring Progress
Solve the system of linear equations by substitution. Check your solution.
Question 1.
y = 3x + 14
y = -4x
Answer:
Given,
y = 3x + 14
y = -4x
-4x = 3x + 14
-4x – 3x = 14
-7x = 14
x = -14/7
x = -2
Substitute x value in y.
y = -4x
y = -4(-2)
y = 8
Check:
y = -4x
8 = -4(-2)
8 = 8
Question 2.
3x + 2y = 0
y = \(\frac{1}{2}\)x – 1
Answer:
3x + 2y = 0
y = \(\frac{1}{2}\)x – 1
\(\frac{1}{2}\)x – y = 1 —- × 2
x – 2y = 2
Solve 1 & 3
3x + 2y = 0
x – 2y = 2
4x = 2
x = 2/4
x = 1/2
3x + 2y = 0
3(\(\frac{1}{2}\)) + 2y = 0
\(\frac{3}{2}\) + 2y = 0
2y = –\(\frac{3}{2}\)
y = –\(\frac{3}{4}\)
Question 3.
x = 6y – 7
4x + y = -3
Answer:
x = 6y – 7
4x + y = -3
x – 6y = -7—– × 4 ⇒ 4x – 24y = -28
4x + y = -3
4x – 24y = -28
4x + y = -3
-25y = -25
y = 1
x – 6y = -7
x – 6(1) = -7
x – 6 = -7
x = -7 + 6
x = -1
Solve the system of linear equations by substitution. Check your solution.
Question 4.
x + y = -2
-3x + y = 6
Answer:
x + y = -2
-3x + y = 6
4x = -8
x = -8/4
x = -2
x + y = -2
-2 + y = -2
y = -2 + 2
y = 0
Check:
x + y = -2
-2 + 0 = -2
-2 = -2
Question 5.
-x + y = -4
4x – y = 10
Answer:
-x + y = -4
4x – y = 10
3x = 6
x = 6/3
x = 2
-x + y = -4
-2 + y = -4
y = -4 + 2
y = -2
Check:
-x + y = -4
-2 + (-2) = -4
-4 = -4
Question 6.
2x – y = -5
3x – y = 1
Answer:
2x – y = -5
3x – y = 1
-x = -6
x = 6
3(6) – y = 1
18 – y = 1
-y = 1 – 18
-y = -17
y = 17
Question 7.
x – 2y = 7
3x – 2y = 3
Answer:
x – 2y = 7
3x – 2y = 3
-2x = 4
x = -2
3x – 2y = 3
3(-2) – 2y = 3
-6 – 2y = 3
-2y = 3 + 6
-2y = 9
y = -9/2
Question 8.
There are a total of 64 students in a drama club and a yearbook club. The drama club has 10 more students than the yearbook club. Write a system of linear equations that represents this situation. How many students are in each club?
Answer:
Given,
There are a total of 64 students in a drama club and a yearbook club.
The drama club has 10 more students than the yearbook club.
x = y + 10
y = 64 – x
y = 64 – (y + 10)
y = 64 – y – 10
y + y = 64 – 10
2y = 54
y = 27
x = y + 10
x = 27 + 10
x = 37
Check:
x + y = 64
37 + 27 = 64
64 = 64
Solving Systems of Linear Equations by Substitution 5.2 Exercises
Vocabulary and Core Concept Check
Question 1.
WRITING
Describe how to solve a system of linear equations by substitution.
Answer: To solve a system of linear equations by substitution, solve one of the equations for one of the variables. Then substitute the expression for this variable into the other equation to find the value of the other variable. Finally, substitute this value into one of the original equations to find the value of the other variable.
Question 2.
NUMBER SENSE
When solving a system of linear equations by substitution, how do you decide which variable to solve for in Step 1?
Answer: The solution does not depend on the choice of variable which is substituted. Any of the two variables can be solved in step 1 and then, substituted in the second equation.
Monitoring Progress and Modeling with Mathematics
In Exercises 3−8, tell which equation you would choose to solve for one of the variables. Explain.
Question 3.
x + 4y = 30
x – 2y = 0
Answer:
Question 4.
3x – y = 0
2x + y = -10
Answer:
Question 5.
5x + 3y = 11
5x – y = 5
Answer:
Question 6.
3x – 2y = 19
x + y = 8
Answer:
Question 7.
x – y = -3
4x + 3y = -5
Answer:
Question 8.
3x + 5y = 25
x – 2y = -6
Answer:
In Exercises 9–16, solve the system of linear equations by substitution. Check your solution.
Question 9.
x = 17 – 4y
y = x – 2
Answer:

Question 10.
6x – 9 = y
y = -3x
Answer:
Question 11.
x = 16 – 4y
3x + 4y = 8
Answer:

Question 12.
-5x + 3y = 51
y = 10x – 8
Answer:
Question 13.
2x = 12
x – 5y = -29
Answer:
Question 14.
2x – y = 23
x – 9 = -1
Answer:
Question 15.
5x + 2y = 9
x + y = -3
Answer:

Question 16.
11x – 7y = -14
x – 2y = -4
Answer:
Given equation is
11x – 7y = -14
x – 2y = -4 —- × 11 ⇒ 11x – 22y = -44
11x – 7y = -14
11x – 22y = -44
15y = 30
y = 2
x – 2y = -4
x – 2(2) = -4
x – 4 = -4
x = -4 + 4
x = 0
Check:
x – 2y = -4
0 – 2 (2) = -4
-4 = -4
Question 17.
ERROR ANALYSIS
Describe and correct the error in solving for one of the variables in the linear system 8x + 2y = -12 and 5x – y = 4.
Answer:
In step 2, the expression for y should be substituted in the other equation.
Step 1:
5x – y = 4
5x – 5x – y = 4 – 5x
-y = 4 – 5x
y = 5x – 4
Step 2:
8x + 2y = -12
8x + 2(5x – 4) = -12
8x + 10x – 8 = -12
18x = -12 + 8
18x = -4
9x = -2
x = -2/9
Question 18.
ERROR ANALYSIS
Describe and correct the error in solving for one of the variables in the linear system 4x + 2y = 6 and 3x + y = 9.
Answer:
Step 3:
3x + y = 9
x = 6
3(6) + y = 9
18 + y = 9
y = 9 – 18
y = -9
Question 19.
MODELING WITH MATHEMATICS
A farmer plants corn and wheat on a 180-acre farm. The farmer wants to plant three times as many acres of corn as wheat. Write a system of linear equations that represents this situation. How many acres of each crop should the farmer plant?
Answer:

Question 20.
MODELING WITH MATHEMATICS
A company that offers tubing trips down a river rents tubes for a person to use and “cooler” tubes to carry food and water. A group spends $270 to rent a total of 15 tubes. Write a system of linear equations that represents this situation. How many of each type of tube does the group rent?
Answer:

In Exercises 21–24, write a system of linear equations that has the ordered pair as its solution.
Question 21.
(3, 5)
Answer:
Question 22.
(-2, 8)
Answer:

Question 23.
(-4, -12)
Answer:
Question 24.
(15, -25)
Answer:

Question 25.
PROBLEM SOLVING
A math test is worth 100 points and has 38 problems. Each problem is worth either 5 points or 2 points. How many problems of each point value are on the test?
Answer:

Question 26.
PROBLEM SOLVING
An investor owns shares of Stock A and Stock B. The investor owns a total of 200 shares with a total value of $4000. How many shares of each stock does the investor own?
Answer:
MATHEMATICAL CONNECTIONS In Exercises 27 and 28, (a) write an equation that represents the sum of the angle measures of the triangle and (b) use your equation and the equation shown to find the values of x and y.
Question 27.
Answer:

Question 28.
Answer:
Question 29.
REASONING
Find the values of a and b so that the solution of the linear system is (-9, 1).
ax + by = -31 Equation 1
ax – by = -41 Equation 2
Answer:

Question 30.
MAKING AN ARGUMENT
Your friend says that given a linear system with an equation of a horizontal line and an equation of a vertical line, you cannot solve the system by substitution. Is your friend correct? Explain.
Answer:
The equation of the vertical line is x = a
The equation of the horizontal line is y = b
We cannot substitute one of the variables into the other equation
Therefore your friend is correct.
Question 31.
OPEN-ENDED
Write a system of linear equations in which (3, -5) is a solution of Equation 1 but not a solution of Equation 2, and (-1, 7) is a solution of the system.
Answer:

Question 32.
HOW DO YOU SEE IT?
The graphs of two linear equations are shown.
a. At what point do the lines appear to intersect?
b. Could you solve a system of linear equations by substitution to check your answer in part (a)? Explain.
Answer:

Question 33.
REPEATED REASONING
A radio station plays a total of 272 pop, rock, and hip-hop songs during a day. The number of pop songs is 3 times the number of rock songs. The number of hip-hop songs is 32 more than the number of rock songs. How many of each type of song does the radio station play?
Answer:

Question 34.
THOUGHT PROVOKING
You have $2.65 in coins. Write a system of equations that represents this situation. Use variables to represent the number of each type of coin.
Answer:
Question 35.
NUMBER SENSE
The sum of the digits of a two-digit number is 11. When the digits are reversed, the number increases by 27. Find the original number
Answer:

Maintaining Mathematical Proficiency
Find the sum or difference.
Question 36.
(x – 4) + (2x – 7)
Answer:
Given expression is (x – 4) + (2x – 7)
x – 4 + 2x – 7
3x – 11
So, (x – 4) + (2x – 7) = 3x – 11
Question 37.
(5y – 12) + (-5y – 1)
Answer:
Given expression is (5y – 12) + (-5y – 1)
5y – 12 – 5y – 1 = -12 – 1 = -13
So, (5y – 12) + (-5y – 1) = -13
Question 38.
(t – 8) – (t + 15)
Answer:
Given expression is
(t – 8) – (t + 15)
t – 8 – t – 15
-8 – 15
-23
So, (t – 8) – (t + 15) = -23
Question 39.
(6d + 2) – (3d – 3)
Answer:
Given expression is (6d + 2) – (3d – 3)
6d + 2 – 3d + 3
3d + 5
So, (6d + 2) – (3d – 3) = 3d + 5
Question 40.
4(m + 2) + 3(6m – 4)
Answer:
Given expression is 4(m + 2) + 3(6m – 4)
4(m) + 4(2) + 3(6m) + 3(-4)
4m + 8 + 18m – 12
22m + 8 – 12
22m – 4
So, 4(m + 2) + 3(6m – 4) = 22m – 4
Question 41.
2(5v + 6) – 6(-9v + 2)
Answer:
Given expression is 2(5v + 6) – 6(-9v + 2)
2(5v) + 2(6) – 6(-9v) – 6(2)
10v + 12 + 54v – 12
64v + 0 = 64v
So, 2(5v + 6) – 6(-9v + 2) = 64v
Lesson 5.3 Solving Systems of Linear Equations by Elimination
Essential Question How can you use elimination to solve a system of linear equations?
EXPLORATION 1
Writing and Solving a System of Equations
Work with a partner. You purchase a drink and a sandwich for $4.50. Your friend purchases a drink and five sandwiches for $16.50. You want to determine the price of a drink and the price of a sandwich.
a. Let x represent the price (in dollars) of one drink. Let y represent the price (in dollars) of one sandwich. Write a system of equations for the situation. Use the following verbal model.
Label one of the equations Equation 1 and the other equation Equation 2.
b. Subtract Equation 1 from Equation 2. Explain how you can use the result to solve the system of equations. Then find and interpret the solution.
Answer:
Given,
You purchase a drink and a sandwich for $4.50.
Your friend purchases a drink and five sandwiches for $16.50.
Let the cost of 1 drink = $x
Let the cost of 1 sandwich = $y
x + y = 4.50
x(1) + y(5) = 16.50
x + 5y = 16.50
x + y – (x + 5y) = 4.50 – 16.50
x + y – x – 5y = -12
-4y = -12
y = 3
Thus the cost of 1 sandwich = $3
x + y = 4.50
x + 3 = 4.50
x = 1.50
So, the cost of 1 drink is $1.50
EXPLORATION 2
Using Elimination to Solve Systems
Work with a partner. Solve each system of linear equations using two methods.
Method 1 Subtract. Subtract Equation 2 from Equation 1. Then use the result to solve the system.
Method 2 Add. Add the two equations. Then use the result to solve the system.
Is the solution the same using both methods? Which method do you prefer?
a. 3x – y = 6
3x + y = 0
Answer:
3x – y = 6
3x + y = 0
3x – y – (3x + y) = 6 – 0
3x – y – 3x – y = 6
-2y = 6
y = -3
3x + y = 0
3x – 3 = 0
3x = 3
x = 1
b. 2x + y = 6
2x – y = 2
Answer:
2x + y = 6
2x – y = 2
4x = 8
x = 8/4
x = 2
2x + y = 6
2(2) + y = 6
4 + y = 6
y = 6 – 4
y = 2
c. x – 2y = -7
x + 2y = 5
Answer:
x – 2y = -7
x + 2y = 5
2x = -2
x = -1
x + 2y = 5
-1 + 2y = 5
2y = 5 + 1
2y = 6
y = 3
EXPLORATION 3
Using Elimination to Solve a System
Work with a partner.
2x + y = 7 Equation 1
x + 5y = 17 Equation 2
a. Can you eliminate a variable by adding or subtracting the equations as they are? If not, what do you need to do to one or both equations so that you can?
b. Solve the system individually. Then exchange solutions with your partner and compare and check the solutions.
Answer:
Given,
2x + y = 7 Equation 1
x + 5y = 17 Equation 2—- × 2
We cannot eliminate by adding or subtracting the equations as they are, we need to multiply equation 2 by 2
2x + y = 7
(-)2x + 10y = 34
-10y = -27
y = 2.7
2x + y = 7
2x + 2.7 = 7
2x = 4.3
x = 2.15
2x + y = 7
2(2.15) + 2.7 = 7
4.3 + 2.7 = 7
7 = 7
So, LHS = RHS
Communicate Your Answer
Question 4.
How can you use elimination to solve a system of linear equations?
Answer:
1. Write given equations in the standard form.
2. Make the coefficients of one variable opposite.
3. Either subtract or add the equations to get an equation in one variable.
Question 5.
When can you add or subtract the equations in a system to solve the system? When do you have to multiply first? Justify your answers with examples.
Answer:
The equations representing the first situation of directly adding or subtracting the equations are
x + y = 5
x – y = 1
Adding equations 1 and 2, we observe that the variable y is eliminated and we are remained with linear equation in single variable
2x = 6
x = 3
Putting this value of x in any of the equations 1 or 2 will get the value of y, and thus we will get the required solution of the system of equations.
3 + y = 5
y = 5 – 3
y = 2
So, the required solution for the system of equations (x, y) = (3, 2)
The equations representing the second situation of multiplying first and then adding or subtracting
2x + 3y = 8 —– × 3
3x + 2y = 7 —- × 4
6x + 9y = 24
6x + 4y = 14
5y = 10
y = 2
3x + 2y = 7
3x + 2(2) = 7
3x + 4 = 7
3x = 7 – 4
3x = 3
x = 1
Thus, the required solution for this system of equations is given by (x, y) = (1, 5).
Question 6.
In Exploration 3, why can you multiply an equation in the system by a constant and not change the solution of the system? Explain your reasoning.
Answer: You need to multiply one or both of the equations by a constant to get the same coefficient.
Monitoring Progress
Solve the system of linear equations by elimination. Check your solution.
Question 1.
3x + 2y = 7
-3x + 4y = 5
Answer:
Given equations
3x + 2y = 7
-3x + 4y = 5
6y = 12
y = 2
3x + 2y = 7
3x + 2(2) = 7
3x + 4 = 7
3x = 7 – 4
3x = 3
x = 1
Check:
3x + 2y = 7
3(1) + 2(2) = 7
3 + 4 = 7
7 = 7
LHS = RHS
Question 2.
x – 3y = 24
3x + y = 12
Answer:
Given equations
x – 3y = 24
3x + y = 12 —- × 3 ⇒ 36x + 3y = 36
x – 3y = 24
9x + 3y = 36
10x = 60
x = 60/10
x = 6
3x + y = 12
3(6) + y = 12
18 + y = 12
y = 12 – 18
y = -6
Check:
3x + y = 12
3(6) + (-6) = 12
18 – 6 = 12
12 = 12
LHS = RHS
Question 3.
x + 4y = 22
4x + y = 13
Answer:
Given equations
x + 4y = 22
4x + y = 13 —- × 4 ⇒ 16x + 4y = 52
x + 4y = 22
16x + 4y = 52
-15x = -30
x = 30/15
x = 2
x + 4y = 22
2 + 4y = 22
4y = 22 – 2
4y = 20
y = 20/4
y = 5
Check:
x + 4y = 22
2 + 4(5) = 22
2 + 20 = 22
22 = 22
LHS = RHS
Question 4.
Solve the system in Example 3 by eliminating x.
Answer:
Solving Systems of Linear Equations by Elimination 5.3 Exercises
Vocabulary and Core Concept Check
Question 1.
OPEN-ENDED
Give an example of a system of linear equations that can be solved by first adding the equations to eliminate one variable.
Answer:
Question 2.
WRITING
Explain how to solve the system of linear equations by elimination.
2x – 3y = -4 Equation 1
-5x + 9y = 7 Equation 2
Answer:

Monitoring Progress and Modeling with Mathematics
In Exercises 3−10, solve the system of linear equations by elimination. Check your solution.
Question 3.
x + 2y = 13
-x + y = 5
Answer:

Question 4.
9x + y = 2
-4x – y = -17
Answer:
Question 5.
5x + 6y = 50
x – 6y = -26
Answer:

Question 6.
-x + y = 4
x + 3y = 4
Answer:


Question 7.
-3x – 5y = -7
-4x + 5y = 14
Answer:

Question 8.
4x – 9y = -21
-4x – 3y = 9
Answer:
Question 9.
-y – 10 = 6x
5x + y = -10
Answer:

Question 10.
3x – 30 = y
7y – 6 = 3x
Answer:



In Exercises 11–18, solve the system of linear equations by elimination. Check your solution.
Question 11.
x + y = 2
2x + 7y = 9
Answer:
Question 12.
8x – 5y = 11
4x – 3y = 5
Answer:



Question 13.
11x – 20y = 28
3x + 4y = 36
Answer:

Question 14.
10x – 9y = 46
-2x + 3y = 10
Answer:


Question 15.
4x – 3y = 8
5x – 2y = -11
Answer:

Question 16.
-2x – 5y = 9
3x + 11y = 4
Answer:


Question 17.
9x + 2y = 39
6x + 13y = -9
Answer:

Question 18.
12x – 7y = -2
8x + 11y = 30
Answer:


Question 19.
ERROR ANALYSIS
Describe and correct the error in solving for one of the variables in the linear system 5x – 7y = 16 and x + 7y = 8.
Answer:
Question 20.
ERROR ANALYSIS
Describe and correct the error in solving for one of the variables in the linear system 4x + 3y = 8 and x – 2y = -13.
Answer:
4x + 3y = 8 and x – 2y = -13.
4x + 3y = 8
x – 2y = -13 —- × 4 ⇒ 4x – 8y = -52
(4x – 4x) – (3y + 4y) = 5
7y = 5
y = 5/7
x – 2y = 13
x – 2(5/7) = 13
x = 13 + 10/7
7x = 91 + 10
7x = 101
x = 101/7
Question 21.
MODELING WITH MATHEMATICS
A service center charges a fee of x dollars for an oil change plus y dollars per quart of oil used. A sample of its sales record is shown. Write a system of linear equations that represents this situation. Find the fee and cost per quart of oil.
Answer:

Question 22.
MODELING WITH MATHEMATICS
A music website charges x dollars for individual songs and y dollars for entire albums. Person A pays $25.92to download 6 individual songs and 2 albums. Person B pays $33.93 to download 4 individual songs and 3 albums. Write a system of linear equations that represents this situation. How much does the website charge to download a song? an entire album?
Answer:
Given,
A music website charges x dollars for individual songs and y dollars for entire albums.
Person A pays $25.92to download 6 individual songs and 2 albums.
Person B pays $33.93 to download 4 individual songs and 3 albums.
The equation is
6x + 2y = 25.92
3x + y = 12.96
y = 12.96 – 3x
4x + 3y = 33.93
4x + 3(12.96 – 3x) = 33.93
4x + 38.88 – 9x = 33.93
-5x = -4.95
x = 0.99 dollars
y = 12.96 – 3x
= 12.96 – 2.97
= 9.99 dollars
In Exercises 23–26, solve the system of linear equations using any method. Explain why you chose the method.
Question 23.
3x + 2y = 4
2y = 8 – 5x
Answer:

Question 24.
-6y + 2 = -4x
y – 2 = x
Answer:



Question 25.
y – x = 2
y = – \(\frac{1}{4}\) x + 7
Answer:
Question 26.
3x + y = \(\frac{1}{3}\)
2x – 3y = \(\frac{8}{3}\)
Answer:



Question 27.
WRITING
For what values of a can you solve the linear system ax + 3y = 2 and 4x + 5y = 6 by elimination without multiplying first? Explain.
Answer:
Question 28.
HOW DO YOU SEE IT?
The circle graph shows the results of a survey in which 50 students were asked about their favorite meal.
a. Estimate the numbers of students who chose breakfast and lunch.
b. The number of students who chose lunch was 5 more than the number of students who chose breakfast. Write a system of linear equations that represents the numbers of students who chose breakfast and lunch.
c. Explain how you can solve the linear system in part (b) to check your answers in part (a).
Answer:



Question 29.
MAKING AN ARGUMENT
Your friend says that any system of equations that can be solved by elimination can be solved by substitution in an equal or fewer number of steps. Is your friend correct? Explain.
Answer:
No, If like terms are in the same respective positions and at least one pair of like terms has the same or opposite coefficients, then elimination is more efficient than substitution and will take fewer steps. On the other hand, if one of the variables in one of the equations is either isolated already or has a coefficient of 1 or -1, then substitution is more efficient and will take fewer steps.
Question 30.
THOUGHT PROVOKING
Write a system of linear equations that can be added to eliminate a variable or subtracted to eliminate a variable.
Answer:



Question 31.
MATHEMATICAL CONNECTIONS
A rectangle has a perimeter of 18 inches. A new rectangle is formed by doubling the width w and tripling the length ℓ, as shown. The new rectangle has a perimeter P of 46 inches.
a. Write and solve a system of linear equations to find the length and width of the original rectangle.
b. Find the length and width of the new rectangle.
Answer:

Question 32.
CRITICAL THINKING
Refer to the discussion of System 1 and System 2 on page 248. Without solving, explain why the two systems shown have the same solution.
Answer:



Question 33.
PROBLEM SOLVING
You are making 6 quarts of fruit punch for a party. You have bottles of 100% fruit juice and 20% fruit juice. How many quarts of each type of juice should you mix to make 6 quarts of 80% fruit juice?
Answer:

Question 34.
PROBLEM SOLVING
A motorboat takes 40 minutes to travel 20 miles downstream. The return trip takes 60 minutes. What is the speed of the current?
Answer:



Question 35.
CRITICAL THINKING
Solve for x, y, and z in the system of equations. Explain your steps.
x + 7y + 3z = 29 Equation 1
3z + x – 2y = -7 Equation 2
5y = 10 – 2x Equation 3
Answer:


Maintaining Mathematical Proficiency
Solve the equation. Determine whether the equation has one solution, no solution, or infinitely many solutions.
Question 36.
5d – 8 = 1 + 5d
Answer:

Question 37.
9 + 4t = 12 – 4t
Answer:
Question 38.
3n + 2 = 2(n – 3)
Answer:
Question 39.
-3(4 – 2v) = 6v – 12
Answer:
Write an equation of the line that passes through the given point and is parallel to the given line.
Question 40.
(4, -1); y = -2x + 7
Answer:


Question 41.
(0, 6); y = 5x – 3
Answer:
Question 42.
(-5, -2); y = \(\frac{2}{3}\)x + 1
Answer:


Lesson 5.4 Solving Special Systems of Linear Equations
Essential Question Can a system of linear equations have no solution or infinitely many solutions?
EXPLORATION 1
Using a Table to Solve a System
Work with a partner. You invest $450 for equipment to make skateboards. The materials for each skateboard cost $20. You sell each skateboard for $20.
a. Write the cost and revenue equations. Then copy and complete the table for your cost C and your revenue R.
b. When will your company break even? What is wrong?
Answer:
Total investment = $540
Cost of one skateboard = $20
Selling Price of one skateboard = $20
Number of skateboard = x
C = Total investment + (cost of one skateboard × number of skateboards)
C = 450 + 20x
R = Selling price of one skateboard × number of skateboards
R = 20x
For x = 0
C = 450
R = 0
For x = 1
C = 450 + 20
C = 470
For x = 2
C = 450 + 40 = 490
R = 40
For x = 3
C = 450 + 60 = 510
R = 60
For x = 4
C = 450 + 80 = 530
R = 80
For x = 5
C = 450 + 100 = 550
R = 100
For x = 6
C = 450 + 120 = 570
R = 120
For x = 7
C = 450 + 140 = 590
R = 140
For x = 8
C = 450 + 160 = 610
R = 160
For x = 9
C = 450 + 180 = 630
R = 180
For x = 10
C = 450 + 200 = 650
R = 200
b. C = 450 + 20x
R = 20x
Profit made by selling one skateboard = $20 – $20 = 0
There is no profit because the cost price and selling price are the same.
There is an additional investment cost of $450.
Thus the revenue for each board must be higher.
EXPLORATION 2
Writing and Analyzing a System
Work with a partner. A necklace and matching bracelet have two types of beads. The necklace has 40 small beads and 6 large beads and weighs 10 grams. The bracelet has 20 small beads and 3 large beads and weighs 5 grams. The threads holding the beads have no significant weight.
a. Write a system of linear equations that represents the situation. Let x be the weight (in grams) of a small bead and let y be the weight (in grams) of a large bead.
Answer:
A system of linear equations that represents the situation of necklace.
Let x be the weight of a small bead and let y be the weight of a large bead.
40x + 6y = 10
A system of linear equations that represents the situation of bracelet.
Let x be the weight of a small bead and let y be the weight of a large bead
20x + 3y = 5
b. Graph the system in the coordinate plane shown. What do you notice about the two lines?
Answer:
40x + 6y = 10 and 20x + 3y = 5
| x | 1 | -0.5 |
| y | -5 | 5 |

c. Can you find the weight of each type of bead? Explain your reasoning.
Answer:
Given a necklace and matching bracelet have two types of beads. The necklace has 40 small beads and 6 large beads and weighs 10 grams. The bracelet has 20 small beads and 3 large beads and weighs 5 grams. The threads holding the beads have no significant weight.
Yes, we can find the weight of each type of bead here we can see that these intersect at infinitely many point so every point graph is the weight of beats.
Communicate Your Answer
Question 3.
Can a system of linear equations have no solution or infinitely many solutions? Give examples to support your answers.
Answer:
A system of linear equations can have infinitely many solutions or no solution.
Example:
4x + 3y = 9
4x + 3y = -7
It has no solution
4x + 3y = 9
8x + 6y = 18
It has infinitely many solutions.
Question 4.
Does the system of linear equations represented by each graph have no solution, one solution, or infinitely many solutions? Explain.
Answer:
a. y = x + 2
x + y = 2
x – y + 2 = 0
x + y – 2 = 0
x = 0
It has one solution.
b. y = x + 2
-x + y = 1
y = x + 2
y = x + 1
It has no solution.
c. y = x + 2
-2x + 2y = 4 ⇒ -x + y = 2
y = x + 2
y = x + 2
2y = 2x + 4
It has infinite solutions.
Monitoring Progress
Solve the system of linear equations.
Question 1.
x + y = 3
2x + 2y = 6
Answer:
Given equations
x + y = 3
2x + 2y = 6 ⇒ x + y = 3
x + y = 3
x + y = 3
x + y – x – y = 3 – 3
0 = 0
It has infinitely many solutions.
Question 2.
y = -x + 3
2x + 2y = 4
Answer:
y = -x + 3
2x + 2y = 4
x + y = 3
2x + 2y = 4 ⇒ x + y = 2
x + y = 3
x + y = 2
It has no solution.
Question 3.
x + y = 3
x + 2y = 4
Answer:
x + y = 3
x + 2y = 4
x + y – x – 2y = 3 – 4
-y = -1
y = 1
It has one solution.
Question 4.
y = -10x + 2
10x + y = 10
Answer:
y = -10x + 2 ⇒ 10x + y = 2
10x + y = 10
10x + y – 10x – y = 2 – 10
0 = -8
It has no solution.
Question 5.
WHAT IF?
What happens to the solution in Example 3 when the perimeter of the trapezoidal piece of land is 96 kilometers? Explain.
Answer:
The trapezoidal land is changed from 48 kilometers to 96 kilometers.
6x + 12y = 96 and 18x + 36y = 144
18x + 36y = 188
18x + 36y – (18x + 36y) = 288 – 144
18x + 36y – 18x – 36y = 144
0 ≠ 144
Therefore, there is no solution to the given system of linear equations.
Solving Special Systems of Linear Equations 5.4 Exercises
Vocabulary and Core Concept Check
Question 1.
REASONING
Is it possible for a system of linear equations to have exactly two solutions? Explain.
Answer: Two lines cannot intersect at exactly two points. So, a system of linear equations cannot have exactly two solutions.
Question 2.
WRITING
Compare the graph of a system of linear equations that has infinitely many solutions and the graph of a system of linear equations that has no solution.
Answer:
Monitoring Progress and Modeling with Mathematics
In Exercises 3−8, match the system of linear equations with its graph. Then determine whether the system has one solution, no solution, or infinitely many solutions.
Question 3.
-x + y = 1
x – y = 1
Answer:

Question 4.
2x – 2y = 4
-x + y = -2
Answer:
Given equations
2x – 2y = 4
-x + y = -2 —- × 2 ⇒ -2x + 2y = -4
2x – 2y = 4
-2x + 2y = -4
0 = 0
It has an infinite number of solutions.
Question 5.
2x + y = 4
-4x – 2y = -8
Answer:

Question 6.
x – y = 0
5x – 2y = 6
Answer:
Given equations
x – y = 0 — × 2 ⇒ 2x – 2y = 0
5x – 2y = 6
2x – 2y = 0
5x – 2y = 6
-3x = -6
x = 2
Substitute x in eq. (1)
x – y = 0
2 – y = 0
y = 2
It has one solution.
Question 7.
-2x + 4y = 1
3x – 6y = 9
Answer:
Question 8.
5x + 3y = 17
x – 3y = -2
Answer:

Graph C is the correct answer. Use the Geogebra calculator to find the linear equation.
In Exercises 9–16, solve the system of linear equations.
Question 9.
y = -2x – 4
y = 2x – 4
Answer:
Question 10.
y = -6x – 8
y = -6x + 8
Answer:

Question 11.
3x – y = 6
-3x + y = -6
Answer:
Question 12.
-x + 2y = 7
x – 2y = 7
Answer:

Question 13.
4x + 4y = -8
-2x – 2y = 4
Answer:
Question 14.
15x – 5y = -20
-3x + y = 4
Answer:

Question 15.
9x – 15y = 24
6x – 10y = -16
Answer:
Question 16.
3x – 2y = -5
4x + 5y = 47
Answer:


In Exercises 17–22, use only the slopes and y-intercepts of the graphs of the equations to determine whether the system of linear equations has one solution, no solution, or infinitely many solutions. Explain.
Question 17.
y = 7x + 13
-21x + 3y = 39
Answer:
Question 18.
y = -6x – 2
12x + 2y = -6
Answer:




Question 19.
4x + 3y = 27
4x – 3y = -27
Answer:
Question 20.
-7x + 7y = 1
2x – 2y = -18
Answer:




Question 21.
-18x + 6y = 24
3x – y = -2
Answer:
Question 22.
2x – 2y = 16
3x – 6y = 30
Answer:



ERROR ANALYSIS In Exercises 23 and 24, describe and correct the error in solving the system of linear equations.
Question 23.
Answer:

Question 24.
Answer:

Question 25.
MODELING WITH MATHEMATICS
A small bag of trail mix contains 3 cups of dried fruit and 4 cups of almonds. A large bag contains 4\(\frac{1}{2}\) cups of dried fruit and 6 cups of almonds. Write and solve a system of linear equations to find the price of 1 cup of dried fruit and 1 cup of almonds.
Answer:
Question 26.
MODELING WITH MATHEMATICS
In a canoe race, Team A is traveling 6 miles per hour and is 2 miles ahead of Team B. Team B is also traveling 6 miles per hour. The teams continue traveling at their current rates for the remainder of the race. Write a system of linear equations that represents this situation. Will Team B catch up to Team A? Explain.
Answer:

Question 27.
PROBLEM SOLVING
A train travels from New York City to Washington, D.C., and then back to New York City. The table shows the number of tickets purchased for each leg of the trip. The cost per ticket is the same for each leg of the trip. Is there enough information to determine the cost of one coach ticket? Explain.
Answer:

Question 28.
THOUGHT PROVOKING
Write a system of three linear equations in two variables so that any two of the equations have exactly one solution, but the entire system of equations has no solution.
Answer:



Question 29.
REASONING
In a system of linear equations, one equation has a slope of 2 and the other equation has a slope of –\(\frac{1}{3}\). How many solutions does the system have? Explain.
Answer:
Question 30.
HOW DO YOU SEE IT?
The graph shows information about the last leg of a 4 × 200-meter relay for three relay teams. Team A’s runner ran about 7.8 meters per second, Team B’s runner ran about 7.8 meters per second, and Team C’s runner ran about 8.8 meters per second.
a. Estimate the distance at which Team C’s runner passed Team B’s runner.
b. If the race was longer, could Team C’s runner have passed Team A’s runner? Explain.
c. If the race was longer, could Team B’s runner have passed Team A’s runner? Explain.
Answer:


Question 31.
ABSTRACT REASONING
Consider the system of linear equations y = ax + 4 and y = bx – 2, where a and b are real numbers. Determine whether each statement is always, sometimes, or never true. Explain your reasoning.
a. The system has infinitely many solutions.
b. The system has no solution.c. When a < b, the system has one solution.
Answer:
Question 32.
MAKING AN ARGUMENT
One admission to an ice skating rink costs x dollars, and renting a pair of ice skates costs y dollars. Your friend says she can determine the exact cost of one admission and one skate rental. Is your friend correct? Explain.
Answer:

Maintaining Mathematical Proficiency
Solve the equation. Check your solutions.
Question 33.
|2x + 6| = |x|
Answer:
Question 34.
|3x – 45| = |12x|
Answer:


Question 35.
|x – 7| = |2x – 8|
Answer:

Question 36.
|2x + 1| = |3x – 11|
Answer:

Solving Systems of Linear Equations Study Skills: Analyzing Your Errors
5.1 – 5.4 What Did You Learn?
Core Vocabulary
system of linear equations, p. 236
solution of a system of linear equations, p. 236
Core Concepts
Section 5.1
Solving a System of Linear Equations by Graphing, p. 237
Section 5.2
Solving a System of Linear Equations by Substitution, p. 242
Section 5.3
Solving a System of Linear Equations by Elimination, p. 248
Section 5.4
Solutions of Systems of Linear Equations, p. 254
Mathematical Practices
Question 1.
Describe the given information in Exercise 33 on page 246 and your plan for finding the solution.
Answer:
Question 2.
Describe another real-life situation similar to Exercise 22 on page 251 and the mathematics that you can apply to solve the problem.
Answer:
Question 3.
What question(s) can you ask your friend to help her understand the error in the statement she made in Exercise 32 on page 258?
Answer:
Study Skills: Analyzing Your Errors
Study Errors
What Happens: You do not study the right material or you do not learn it well enough to remember it on a test without resources such as notes.
How to Avoid This Error: Take a practice test. Work with a study group. Discuss the topics on the test with your teacher. Do not try to learn a whole chapter’s worth of material in one night.
Solving Systems of Linear Equations 5.1–5.4 Quiz
Use the graph to solve the system of linear equations. Check your solution.
Question 1.
y = – \(\frac{1}{3}\)x + 2
y = x – 2
Answer:
Given equations
y = – \(\frac{1}{3}\)x + 2
y = x – 2
\(\frac{1}{3}\)x + y = 2
x – y = 2
\(\frac{4}{3}\)x = 4
4x = 12
x = 12/4
x = 3
y = x – 2
y = 3 – 2
y = 1
So, the solution is (3, 1).
Question 2.
y = \(\frac{1}{2}\)x – 1
y = 4x + 6
Answer:
Given equations
y = \(\frac{1}{2}\)x – 1
y = 4x + 6
\(\frac{1}{2}\)x – y = 1
4x – y = -6
-3\(\frac{1}{2}\)x = 7
–\(\frac{7}{2}\)x = 7
-7x = 14
x = -14/7
x = -2
y = 4x + 6
y = 4(-2) + 6
y = -8 + 6
y = -2
The solution is (-2, 2)
Question 3.
y = 1
y = 2x + 1
Answer:
Given equations
y = 1
y = 2x + 1
1 = 2x + 1
2x = 0
x = 0
The solution is (0, 1).
Solve the system of linear equations by substitution. Check your solution.
Question 4.
y = x – 4
-2x + y = 18
Answer:
Given equations
y = x – 4
-2x + y = 18
x – y = 4
-2x + y = 18
-x = 22
x = -22
y = -22 – 4
y = -26
Check:
-26 = -22 – 4
-26 = -26
The solution is correct.
Question 5.
2y + x = -4
y – x = -5
Answer:
Given equations
2y + x = -4
y – x = -5
3y = -9
y = -9/3
y = -3
-3 – x = -5
-x = -5 + 3
-x = -2
x = 2
Check:
2y + x = -4
2(-3) + 2 = -4
-6 + 2 = -4
-4 = -4
Question 6.
3x – 5y = 13
x + 4y = 10
Answer:
Given equations
3x – 5y = 13
x + 4y = 10 —- × 3 ⇒ 3x + 12y = 30
3x – 5y = 13
3x + 12y = 30
-17y = -17
y = 1
x + 4y = 10
x + 4(1) = 10
x + 4 = 10
x = 10 – 4
x = 6
Check:
6 + 4(1) = 10
6 + 4 = 10
10 = 10
Solve the system of linear equations by elimination. Check your solution.
Question 7.
x + y = 4
-3x – y = -8
Answer:
Given equations
x + y = 4
-3x – y = -8
-2x = -4
x = 2
2 + y = 4
y = 4 – 2
y = 2
Check:
x + y = 4
2 + 2 = 4
4 = 4
Question 8.
x + 3y = 1
5x + 6y = 14
Answer:
x + 3y = 1 —- × 2
5x + 6y = 14
2x + 6y = 2
5x + 6y = 14
-3x = -12
x = 4
4 + 3y = 1
3y = 1 – 4
3y = -3
y = -1
Check:
2x + 6y = 2
2(4) + 6(-1) = 2
8 – 6 = 2
2 = 2
Question 9.
2x – 3y = -5
5x + 2y = 16
Answer:
Given equations
2x – 3y = -5 — × 5 ⇒ 10x – 15y = -15
5x + 2y = 16 — × 2 ⇒ 10x + 4y = 32
10x – 15y = -25
(-)10x + 4y = 32
-19y = -57
y = 3
5x + 2(3) = 16
5x + 6 = 16
5x = 16 – 6
5x = 10
x = 2
Check:
5x + 2y = 16
5(2) + 2(3) = 16
10 + 6 = 16
16 = 16
LHS = RHS
Solve the system of linear equations.
Question 10.
x – y = 1
x – y = 6
Answer:
x – y = 1
(-)x – y = 6
0 = 7
It has no solution.
Question 11.
6x + 2y = 16
2x – y = 2
Answer:
Given equation
6x + 2y = 16
2x – y = 2 —- × 2 ⇒ 4x – 2y = 4
6x + 2y = 16
4x – 2y = 4
10x = 20
x = 20/10
x = 2
4x – 2y = 4
4(2) – 2y = 4
8 – 2y = 4
8 – 4 = 2y
2y = 4
y = 2
Check:
4x – 2y = 4
4(2) – 2(2) = 4
8 – 4 = 4
4 = 4
LHS = RHS
Question 12.
3x – 3y = -2
-6x + 6y = 4
Answer:
3x – 3y = -2 —- × 2 ⇒ 6x – 6y = -4
-6x + 6y = 4
6x – 6y = -4
-6x + 6y = 4
0 = 0
It has no solution.
Question 13.
You plant a spruce tree that grows 4 inches per year and a hemlock tree that grows 6 inches per year. The initial heights are shown.
a. Write a system of linear equations that represents this situation.
b. Solve the system by graphing. Interpret your solution.
Answer:
Spruce Tree:
Initial Height = 8
Growth = 4
Hemlock Tree:
Initial Height = 14
Growth = 6
Equation = Initial height + Growth × x
s(x) = 8 + 4x
h(x) = 14 + 6x
Question 14.
It takes you 3 hours to drive to a concert 135 miles away. You drive 55 miles per hour on highways and 40 miles per hour on the rest of the roads.
a. How much time do you spend driving at each speed?
b. How many miles do you drive on highways? the rest of the roads?
Answer:
Given,
It takes you 3 hours to drive to a concert 135 miles away.
You drive 55 miles per hour on highways and 40 miles per hour on the rest of the roads.
Let x be the number of hour taken to drive on highway and y be the number of hour taken to drive on the rest of the road.
55x + 40y = 135 —- (1)
x + y = 3 —–(2) —- 55
55x + 55y = 165
55x + 40y = 135
-10y = -15
y = 1.5
Hence 1.5 hours is spend to drive to speed of 55 miles per hour and 1.5 hours are spend to drive for 45 miles per hour.
Question 15.
In a football game, all of the home team’s points are from 7-point touchdowns and 3-point field goals. The team scores six times. Write and solve a system of linear equations to find the numbers of touchdowns and field goals that the home team scores.
Answer:
Given,
In a football game, all of the home team’s points are from 7-point touchdowns and 3-point field goals. The team scores six times.
x + y = 6
Total score is 26.
Score from touchdown goals is 7x
Score from point field goal is 3y.
7x + 3y = 26
x + y = 6 and 7x + 3y = 26.
7(6 – y) + 3y = 26
42 – 7y + 3y = 26
42 – 4y = 26
-4y = -16
y = 4
x + y = 6
x + 4 = 6
x = 2
So the solution (x, y) is (2, 4).
Lesson 5.5 Solving Equations by Graphing
Essential Question How can you use a system of linear equations to solve an equation with variables on both sides?
Previously, you learned how to use algebra to solve equations with variables on both sides. Another way is to use a system of linear equations.
EXPLORATION 1
Solving an Equation by Graphing
Work with a partner. Solve 2x – 1 = – \(\frac{1}{2}\) x + 4 by graphing.
a. Use the left side to write a linear equation. Then use the right side to write another linear equation.
b. Graph the two linear equations from part (a). Find the x-value of the point of intersection. Check that the x-value is the solution of
2x – 1 = –\(\frac{1}{2}\)x + 4.
c. Explain why this “graphical method” works.
Answer:
a. 2x – 1 = –\(\frac{1}{2}\)x + 4
y = 2x – 1
Separate two of the equation on either side of the equal to sign by using another variable y.
y = –\(\frac{1}{2}\)x + 4
b. 2x – 1 = –\(\frac{1}{2}\)x + 4
y = 2x – 1 —-(1)
y = –\(\frac{1}{2}\)x + 4 —- (2)
2x – 1 =–\(\frac{1}{2}\)x + 4
2x + \(\frac{x}{2}\) – 1 = \(\frac{-x}{2}\) + \(\frac{x}{2}\) + 4
\(\frac{5x}{2}\) – 1 = 4
\(\frac{5x}{2}\) – 1 + 1 = 4 + 1
\(\frac{5x}{2}\)/\(\frac{5x}{2}\) = 5/\(\frac{5x}{2}\)
x = 2
y = 2(2) – 1
y = 4 – 1
y = 3
So, the graph intersects at (2, 3).
EXPLORATION 2
Solving Equations Algebraically and Graphically
Work with a partner. Solve each equation using two methods.
Method 1 Use an algebraic method.
Method 2 Use a graphical method.
Is the solution the same using both methods?
a. \(\frac{1}{2}\)x + 4 = –\(\frac{1}{4}\)x + 1
b. \(\frac{2}{3}\)x + 4 = \(\frac{1}{3}\)x + 3
c. –\(\frac{2}{3}\) x – 1 = \(\frac{1}{3}\)x – 4
d. \(\frac{4}{5}\) x + \(\frac{7}{5}\) = 3x – 3
e. -x + 2.5 = 2x – 0.5
f. – 3x + 1.5 = x + 1.5
Answer:
a. \(\frac{1}{2}\)x + 4 = –\(\frac{1}{4}\)x + 1
Given,
\(\frac{1}{2}\)x + 4 = –\(\frac{1}{4}\)x + 1
Adding \(\frac{1}{4}\)x on both sides
\(\frac{3}{4}\)x + 4 = 1
\(\frac{3}{4}\)x = -3
3x = -12
x = -12/3
x = -4
y = \(\frac{1}{2}\)x + 4
y = –\(\frac{1}{4}\)x + 1
y = \(\frac{1}{2}\)x + 4
x = 0
y = \(\frac{1}{2}\)(0) + 4
y = 4
Coordinates: (0, 4)
Put x = 1
y = \(\frac{1}{2}\)(1) + 4
y = \(\frac{1}{2}\) + 4
y = 4.5
Coordinates: (1, 4.5)
y = –\(\frac{1}{4}\)x + 1
put x = 0
y = –\(\frac{1}{4}\)(0) + 1
y = 1
Coordinates: (0, 1)
Put x = 1
y = –\(\frac{1}{4}\)(1) + 1
y = -0.25 + 1
y = 0.75
Coordinates: (1, 0.75)
b. \(\frac{2}{3}\)x + 4 = \(\frac{1}{3}\)x + 3
\(\frac{2}{3}\)x + 4 = \(\frac{1}{3}\)x + 3
\(\frac{2}{3}\)x + 4 – \(\frac{1}{3}\)x = 3
\(\frac{1}{3}\)x + 4 – 3 = 0
\(\frac{1}{3}\)x + 1 = 0
\(\frac{1}{3}\)x = -1
x = -1 × 3
x = -3
y = \(\frac{2}{3}\)x + 4
y = \(\frac{1}{3}\)x + 3
y = \(\frac{2}{3}\)x + 4
put x = 0
y = \(\frac{2}{3}\)(0) + 4
y = 4
put x = 1
y = \(\frac{2}{3}\)(1) + 4
y = \(\frac{2}{3}\) + 4
y = 0.67 + 4
y = 4.67
Coordinates: (1, 4.67)
y = \(\frac{1}{3}\)x + 3
put x = 0
y = \(\frac{1}{3}\)(0) + 3
y = 3
Coordinates: (0, 3)
put x = 1
y = \(\frac{1}{3}\)(1) + 3
y = 0.33 + 3
y = 3.33
Coordinates: (1, 3.33)
c. –\(\frac{2}{3}\) x – 1 = \(\frac{1}{3}\)x – 4
–\(\frac{2}{3}\) x – 1 = \(\frac{1}{3}\)x – 4
–\(\frac{2}{3}\) x – 1 – \(\frac{1}{3}\)x = – 4
-1x – 1 = -4
-x = -4 + 1
-x = -3
x = 3
y = –\(\frac{2}{3}\) x – 1
y = \(\frac{1}{3}\)x – 4
y = –\(\frac{2}{3}\) x – 1
put x = 0
y = –\(\frac{2}{3}\) (0) – 1
y = -1
Coordinates: (0, -1)
put x = 1
y = –\(\frac{2}{3}\) (1) – 1
y = -0.67 – 1
y = -1.67
Coordinates: (1, -1.67)
y = \(\frac{1}{3}\)x – 4
put x = 0
y = \(\frac{1}{3}\)(0) – 4
y = -4
Coordinates: (0, -4)
put x = 1
y = \(\frac{1}{3}\)(1) – 4
y = 0.33 – 4
y = -3.66
Coordinates: (1, -3.66)
d. \(\frac{4}{5}\) x + \(\frac{7}{5}\) = 3x – 3
\(\frac{4}{5}\) x + \(\frac{7}{5}\) = 3x – 3
\(\frac{4}{5}\) x + \(\frac{7}{5}\) = 3x – 3
\(\frac{7}{5}\) = \(\frac{11}{5}\) x – 3
\(\frac{22}{5}\) = \(\frac{11}{5}\) x
\(\frac{5}{11}\) × \(\frac{22}{5}\) = \(\frac{5}{11}\) × \(\frac{11}{5}\)x
2 = x
y = \(\frac{4}{5}\) x + \(\frac{7}{5}\)
y = 3x – 3
y = \(\frac{4}{5}\) x + \(\frac{7}{5}\)
put x = 0
y = \(\frac{4}{5}\) (0) + \(\frac{7}{5}\)
y = \(\frac{7}{5}\)
y = 1.4
Coordinates: (0, 1.4)
put x = 1
y = \(\frac{4}{5}\) (1) + \(\frac{7}{5}\)
y = \(\frac{11}{5}\)
y = 2.2
Coordinates: (1, 2.2)
y = 3x – 3
put x = 0
y = 3(0) – 3
y = -3
put x = 1
y = 3(1) – 3
y = 0
Coordinates: (1, 0)
e. -x + 2.5 = 2x – 0.5
-x + 2.5 = 2x – 0.5
-x – 2x = -2.5 – 0.5
-3x = -3
x = 1
y = -x + 2.5
y = 2x – 0.5
y = -x + 2.5
put x = 0
y = 0 + 2.5
y = 2.5
put x = 2
y = -2 + 2.5
y = 0.5
Coordinates: (2, 0.5)
y = 2x – 0.5
x = 0
y = 2(0) – 0.5
y = -0.5
Coordinates: (0, -0.5)
x = 2
y = 2(2) – 0.5
y = 4 – 0.5
y = 3.5
Coordinates: (2, 3.5)
f. – 3x + 1.5 = x + 1.5
– 3x + 1.5 = x + 1.5
1.5 = 4x + 1.5
4x = 0
y = -3x + 1.5 and
y = x + 1.5
y = -3x + 1.5
put x = 2
y = -3(2) + 1.5
y = -6 + 1.5
y = -4.5
Coordinates: (2, -4.5)
put x = 1
y = -3(1) + 1.5
y = -3 + 1.5
y = -1.5
Coordinates: (1, -1.5)
y = x + 1.5
put x = 1
y = 1 + 1.5
y = 2.5
Coordinates: (1, 2.5)
put x = 2
y = 2 + 1.5
y = 3.5
Coordinates: (2, 3.5)
Communicate Your Answer
Question 3.
How can you use a system of linear equations to solve an equation with variables on both sides?
Answer:
1. First we choose left side to be the variable side and then the right will be the constant side.
2. Next we collect the variable terms to the variable side and the constants to the other side, using the addition or subtraction property of equality.
3. Now we make the coefficient of the variable using multiplication or division property of equality.
4. In the final step we substitute this value in the original equation to check the solution.
Question 4.
Compare the algebraic method and the graphical method for solving a linear equation with variables on both sides. Describe the advantages and disadvantages of each method.
Answer: It helps you to graph quickly, having both equations in Y form makes this method useful. In contrast, if neither equation has Y isolated, you are better off using substitution or elimination.
Monitoring Progress
Solve the equation by graphing. Check your solution.
Question 1.
\(\frac{1}{2}\)x – 3 = 2x
Answer:
y = \(\frac{1}{2}\)x – 3 and
y = 2x
Coordinates: (-2, -4)
Question 2.
-4 + 9x = -3x + 2
Answer:
y = -4 + 9x
y = -3x + 2
Coordinates: (0.5, 0.5)
Solve the equation by graphing. Check your solutions.
Question 3.
|2x + 2| = |x – 2|
Answer:
y = |2x + 2| and
y = |x – 2|
Coordinates: (0, 2)
Question 4.
|x – 6| = |-x + 4|
Answer:
y = |x – 6| and
y = |-x + 4|
Coordinates: (5, 1)
Question 5.
WHAT IF?
Company C charges $3.30 per mile plus a flat fee of $115 per week. After how many miles are the total costs the same at Company A and Company C?
Answer:
Given,
Company C charges $3.30 per mile plus a flat fee of $115 per week.
Let x be the number of miles travelled
So, the equation is 3.25x + 125 = 3.30x + 115
y = 3.30x + 125
y = 3.30x + 115
Coordinates = (200, 775)
The total costs are the same after 200 miles.
Solving Equations by Graphing 5.5 Exercises
Vocabulary and Core Concept Check
Question 1.
REASONING
The graphs of the equations y = 3x – 20 and y = -2x + 10 intersect at the point (6, −2). Without solving, find the solution of the equation 3x – 20 = -2x + 10.
Answer:
The graphs of the equations y = 3x – 20 and y = -2x + 10 intersect at the point (6, −2).
x = 6 and y = -2
Question 2.
WRITING
Explain how to rewrite the absolute value equation |2x – 4| = |-5x + 1| as two systems of linear equations.
Answer:
Monitoring Progress and Modeling with Mathematics
In Exercises 3–6, use the graph to solve the equation. Check your solution.
Question 3.
-2x + 3 = x
Answer:
The graphs of y = -2x + 3 and y =x intersect at (1, 1).
Check:
-2x + 3 = x
-2(1) + 3 = 1
-2 + 3 = 1
1 = 1
So, the solution of the original equation is x = 1.
Question 4.
-3 = 4x + 1
Answer:
Intersect at (-1, 0)
-3 = 4x + 1
4x + 4 = y
4(-1) + 4 = y
y = 0
Question 5.
-x – 1 = \(\frac{1}{3}\)x + 3
Answer:
Question 6.
–\(\frac{3}{2}\)x – 2 = -4x + 3
Answer:
y = –\(\frac{3}{2}\)x – 2 and y = -4x + 3
Intersect at (2, 5)
–\(\frac{3}{2}\)x – 2 = -4x + 3
–\(\frac{3}{2}\)(2) – 2 = -4(2) + 3
-3 – 2 = -8 + 3
-5 = -5
So, the solution of the original equation is x = 2.
In Exercises 7−14, solve the equation by graphing. Check your solution.
Question 7.
x + 4 = -x
Answer:
Question 8.
4x = x + 3
Answer:
y = 4x and
y = x + 3
The graph intersects at (1, 4).
4x = x + 3
4(1) = 1 + 3
4 = 4
So, the solution of the original equation is x = 1.
Question 9.
x + 5 = -2x – 4
Answer:
Question 10.
-2x + 6 = 5x – 1
Answer:
-2x + 6 = 5x – 1
y = -2x + 6 and
y = 5x – 1
Intersects at (1, 4)
-2x + 6 = 5x – 1
x = 1
-2(1) + 6 = 5(1) – 1
-2 + 6 – 5 – 1
4 = 4
So, the solution of the original equation is x = 1.
Question 11.
\(\frac{1}{2}\)x – 2 = 9 – 5x
Answer:
Question 12.
-5 + \(\frac{1}{4}\)x = 3x + 6
Answer:
-5 + \(\frac{1}{4}\)x = 3x + 6
y = -5 + \(\frac{1}{4}\)x and
y = 3x + 6
The graph intersects at (-4,-6)
-5 + \(\frac{1}{4}\)x = 3x + 6
x = -4
-5 + \(\frac{1}{4}\)(-4) = 3(-4) + 6
-5 – 1 = -12 + 6
-6 = -6
So, the solution of the original equation is x = -4.
Question 13.
5x – 7 = 2(x + 1)
Answer:
Question 14.
-6(x + 4) = -3x – 6
Answer:
-6(x + 4) = -3x – 6
-6x – 24 = -3x – 6
y = -6x – 24 and
y = -3x – 6
The graph intersects at (-6, 12)
x = -6
-6x – 24 = -3x – 6
-6(-6) – 24 = -3(-6) – 6
36 – 24 = 18 – 6
12 = 12
In Exercises 15−20, solve the equation by graphing. Determine whether the equation has one solution, no solution, or infinitely many solutions.
Question 15.
3x – 1 = -x + 7
Answer:
Question 16.
5x – 4 = 5x + 1
Answer:
The original equation has no solution.
Question 17.
-4(2 – x) = 4x – 8
Answer:
Question 18.
-2x – 3 = 2(x – 2)
Answer:
-2x – 3 = 2(x – 2)
-2x – 3 = 2x – 4
Question 19.
-x – 5 = –\(\frac{1}{3}\) (3x + 5)
Answer:
Question 20.
\(\frac{1}{2}\)(8x + 3) = 4x + \(\frac{3}{2}\)
Answer:
\(\frac{1}{2}\)(8x + 3) = 4x + \(\frac{3}{2}\)
y = \(\frac{1}{2}\)(8x + 3)
y = 4x + \(\frac{3}{2}\)
In Exercises 21 and 22, use the graphs to solve the equation. Check your solutions.
Question 21.
|x – 4| = |3x|
Answer:
Question 22.
|2x + 4| = |x – 1|
Answer:
The first graph intersects at (-5, -6) and the second graph intersects at (-1, 2).
Check:
|2x + 4| = |x – 1|
|2(-5)+4| = |-5-1|
|-10+4| = |-6|
|-6| = |-6|
LHS = RHS
|2x + 4| = |x – 1|
|2(-1)+4| = |-1-1|
|-2+4| = |-2|
|2| = |-2|
2 = 2
In Exercises 23−30, solve the equation by graphing. Check your solutions.
Question 23.
|2x| = |x + 3|
Answer:

Question 24.
|2x – 6| = |x|
Answer:
The graph intersects at (0, 6).
Check:
|2x – 6| = |x|
|2(0) – 6| = |0|
|-6| = |0|
LHS ≠ RHS
The graph intersects at (0, 0).
Check:
|2x – 6| = |x|
|2(0) – 6| = |0|
|-6| = |0|
LHS ≠ RHS
Question 25.
|-x + 4| = |2x – 2|
Answer:

Question 26.
|x + 2| = |-3x + 6|
Answer:
The graph intersects at (0, 2).
Check:
|x + 2| = |-3x + 6|
|0+2| = |-3(0)+6|
2 ≠ 6
The graph intersects at (0, 6)
Check:
|x + 2| = |-3x + 6|
|0+2| = |-3(0)+6|
2 ≠ 6
Question 27.
|x + 1| = |x – 5|
Answer:

Question 28.
|2x + 5| = |-2x + 1|
Answer:
|2x + 5| = |-2x + 1|
Equation 1 intersects at (-1,3) and equation 2 intersects at (0,1).
Check:
|2x + 5| = |-2x + 1|
|2(-1) + 5| = |-2(-1) + 1|
-2+5 = 2 + 1
3 = 3
x = 0
|2x + 5| = |-2x + 1|
|2(0)+5| = |-2(0)+1|
5 ≠ 1
Question 29.
|x – 3| = 2|x|
Answer:

Question 30.
4|x + 2| = |2x + 7|
Answer:
4|x + 2| = |2x + 7|
USING TOOLS In Exercises 31 and 32, use a graphing calculator to solve the equation.
Question 31.
0.7x + 0.5 = -0.2x – 1.3
Answer:
Question 32.
2.1x + 0.6 = -1.4x + 6.9
Answer:
Given,
2.1x + 0.6 = -1.4x + 6.9
2.1x + 1.4x = 6.9 – 0.6
3.5x = 6.3
x = 6.3/3.5
x = 1.8
The solution is x = 1.8
Question 33.
MODELING WITH MATHEMATICS
You need to hire a catering company to serve meals to guests at a wedding reception. Company A charges $500 plus $20 per guest. Company B charges $800 plus $16 per guest. For how many guests are the total costs the same at both companies?
Answer:
Question 34.
MODELING WITH MATHEMATICS
Your dog is 16 years old in dog years. Your cat is 28 years old in cat years. For every human year, your dog ages by 7 dog years and your cat ages by 4 cat years. In how many human years will both pets be the same age in their respective types of years?
Answer:
Given,
Your dog is 16 years old in dog years. Your cat is 28 years old in cat years.
For every human year, your dog ages by 7 dog years and your cat ages by 4 cat years.
16 + 7x = 28 + 4x
y = 16 + 7x
y = 28 + 4x
The point of intersection is (4, 44)
16 + 7(4) = 28 + 4(4)
44 = 44
So, in 4 years, human years will both pets be the same age in their respective types of years.
Question 35.
MODELING WITH MATHEMATICS
You and a friend race across a field to a fence and back. Your friend has a 50-meter head start. The equations shown represent you and your friend’s distances d (in meters) from the fence t seconds after the race begins. Find the time at which you catch up to your friend.
You: d = |-5t + 100|
Your friend: d = |-3\(\frac{1}{3}\)t + 50|
Answer:
Question 36.
MAKING AN ARGUMENT
The graphs of y = -x + 4 and y = 2x – 8 intersect at the point (4, 0). So, your friend says the solution of the equation -x + 4 = 2x – 8 is (4, 0). Is your friend correct? Explain.
Answer:
Given,
The graphs of y = -x + 4 and y = 2x – 8 intersect at the point (4, 0).
So, your friend says the solution of the equation -x + 4 = 2x – 8 is (4, 0).
-x + 4 = 2x – 8
-x + 4 – (4 + 2x) = 2x – 8 – (4 + 2x)
-3x = -12
x = 4
So, the solution is x = 4.
Question 37.
OPEN-ENDED
Find values for m and b so that the solution of the equation mx + b = – 2x – 1 is x = -3.
Answer:
Question 38.
HOW DO YOU SEE IT?
The graph shows the total revenue and expenses of a company x years after it opens for business.
a. Estimate the point of intersection of the graphs.
b. Interpret your answer in part (a).
Answer:
a. The red line passes through (2, 4) & (5, 5).
y – y1/x – x1 = y2 – y1/x2 – x1
⇒y – 4/x – 2 = 5 – 4/5 – 2
3(y – 4) = x – 2
3y – 12 = x – 2
3y – 12 = x – 2
x – 3y + 10 = 0
The blue line passes through (1, 1) & (4, 3)
y – y1/x – x1 = y2 – y1/x2 – x1
y – 1/x – 1 = 3 – 1/4 – 1
3(y – 1) = 2(x – 1)
3y – 3 = 2x – 2
2x – 3y + 1 = 0
x = 3y – 10
2(3y – 10) – 3y + 1 = 0
3y = 19
y = 19/3
x = 3 × (19/3) – 10
x = 19 – 10
x = 9
The intersecting points = (9, 19/3)
b. From the graph we can see that x & y axis represents time and amount of money respectively.
19/3 = 6.3 million dollars.
Question 39.
MATHEMATICAL CONNECTIONS
The value of the perimeter of the triangle (in feet) is equal to the value of the area of the triangle (in square feet). Use a graph to find x.
Answer:
Question 40.
THOUGHT PROVOKING
A car has an initial value of $20,000 and decreases in value at a rate of $1500 per year. Describe a different car that will be worth the same amount as this car in exactly 5 years. Specify the initial value and the rate at which the value decreases.
Answer:
Given,
A car has an initial value of $20,000 and decreases in value at a rate of $1500 per year.
Describe a different car that will be worth the same amount as this car in exactly 5 years.
1500 × 5 = $7,500
v = -7500y + 20,000
Question 41.
ABSTRACT REASONING
Use a graph to determine the sign of the solution of the equation ax + b = cx + d in each situation.
a. 0 < b < d and a < c
b. d < b < 0 and a < c Answer: Maintaining Mathematical Proficiency Graph the inequality.
Answer:

Question 42.
y > 5
Answer:
Question 43.
x ≤ -2
Answer:
Question 44.
n ≥ 9
Answer:
Question 45.
c < -6
Answer:
Use the graphs of f and g to describe the transformation from the graph of f to the graph of g.
Question 46.
f(x) = x – 5; g(x) = f(x + 2)
Answer:
x = -1
f(x) = x – 5
= (-1) – 5
= -1 – 5 = -6
x = 0
= (0) – 5 = -5
x = 1
= 1 – 5 = -4
g(x) = f(x + 2)
x = 0
f(0+2) = f(2)
= 2 – 5 = -3
x = 1
f(1 + 2) = f(3)
= 3 – 5 = -2
Question 47.
f(x) = 6x; g(x) = -f(x)
Answer:
Question 48.
f(x) = -2x + 1; g(x) = f(4x)
Answer:
f(x) = -2x + 1;
x = 0
f(0) = -2(0) + 1 = 1
f(1) = -2(1) + 1 = -2 + 1 = -1
f(-1) = -2(-1) + 1 = 2 + 1 = 3
Question 49.
f(x) = \(\frac{1}{2}\)x – 2; g(x) = f(x – 1)
Answer:
Lesson 5.6 Graphing Linear Inequalities in Two Variables
Essential Question How can you graph a linear inequality in two variables?
A solution of a linear inequality in two variables is an ordered pair (x, y) that makes the inequality true. The graph of a linear inequality in two variables shows all the solutions of the inequality in a coordinate plane.
EXPLORATION 1
Writing a Linear Inequality in Two Variables
Work with a partner.
a. Write an equation represented by the dashed line.
b. The solutions of an inequality are represented by the shaded region. In words, describe the solutions of the inequality.
c. Write an inequality represented by the graph. Which inequality symbol did you use? Explain your reasoning.
EXPLORATION 2
Using a Graphing Calculator
Work with a partner. Use a graphing calculator to graph y ≥ \(\frac{1}{4}\)x – 3.
a. Enter the equation y = \(\frac{1}{4}\)x – 3 into your calculator.
b. The inequality has the symbol ≥. So, the region to be shaded is above the graph of y = \(\frac{1}{4}\)x – 3, as shown. Verify this by testing a point in this region, such as (0, 0), to make sure it is a solution of the inequality.
Because the inequality symbol is greater than or equal to, the line is solid and not dashed. Some graphing calculators always use a solid line when graphing inequalities. In this case, you have to determine whether the line should be solid or dashed, based on the inequality symbol used in the original inequality
Answer:
EXPLORATION 3
Graphing Linear Inequalities in Two Variables
Work with a partner. Graph each linear inequality in two variables. Explain your steps. Use a graphing calculator to check your graphs.
a. y > x + 5
b. y ≤ –\(\frac{1}{2}\)x + 1
c. y ≥ -x – 5
Answer:
a. y > x + 5
b. y ≤ –\(\frac{1}{2}\)x + 1
c. y ≥ -x – 5
Communicate Your Answer
Question 4.
How can you graph a linear inequality in two variables?
Answer:
We need to plot the line y = ax + b.
According to given symbols we need a pick point form graph and put it in the inequality is a condition that arises is true then the region of the point is shaded and it represents the inequality.
All the points lying on the shaded region of inequality are its solutions.
Question 5.
Give an example of a real-life situation that can be modeled using a linear inequality in two variables.
Answer:
Example: If we have a total of $50 that could be spent on kiwi and apples which are $25/kg and $30/kg for making a desert, then we have to find the linear inequation in two variables of how much would be the quality that we should buy that would not exceed the budget.
Amount of kiwi . Rate of kiwi + amount of apples . rate of apples ≤ 50
Monitoring Progress
Tell whether the ordered pair is a solution of the inequality.
Question 1.
x + y > 0; (-2, 2)
Answer:
x + y > 0
The ordered pair = (-2, 2)
-2 + 2 > 0
0 > 0
It is not the solution to inequality.
Question 2.
4x – y ≥ 5; (0, 0)
Answer:
4x – y ≥ 5
4(0) – 0 ≥ 5
0 ≥ 5
It is not the solution to inequality.
Question 3.
5x – 2y ≤ -1; (-4, -1)
Answer:
5x – 2y ≤ -1
(-4, -1)
5(-4) – 2(-1) ≤ -1
-20 + 2 ≤ -1
-18 ≤ -1
It is the solution to inequality.
Question 4.
-2x – 3y < 15; (5, -7)
Answer:
-2x – 3y < 15; (5, -7)
-2(5) – 3(-7) < 15
-10 + 21 < 15
11 < 15
It is the solution to inequality.
Graph the inequality in a coordinate plane.
Question 5.
y > -1
Answer:
Question 6.
x ≤ -4
Answer:
Question 7.
x + y ≤ -4
Answer:
Question 8.
x – 2y < 0
Answer:
Question 9.
You can spend at most $12 on red peppers and tomatoes for salsa. Red peppers cost $4 per pound, and tomatoes cost $3 per pound. Write and graph an inequality that represents the amounts of red peppers and tomatoes you can buy. Identify and interpret two solutions of the inequality.
Answer:
Given,
You can spend at most $12 on red peppers and tomatoes for salsa.
Red peppers cost $4 per pound, and tomatoes cost $3 per pound.
4x + 3y ≥ 12
Graphing Linear Inequalities in Two Variables 5.6 Exercises
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
How can you tell whether an ordered pair is a solution of a linear inequality?
Answer:
To tell whether an ordered pair is a solution to a linear inequality, substitute the values into the linear inequality. If they make the inequality true, then the ordered pair is a solution to the linear inequality. If they make the inequality false, then the ordered pair is not a solution to the linear inequality.
Question 2.
WRITING
Compare the graph of a linear inequality in two variables with the graph of a linear equation in two variables.
Answer:
The general linear equation in two variables is ax + by + c = 0 where a, b, c are constants.
To find the graph of ax + bx + c = 0, assume a set of values for x and calculate the respective set of values for y.
The coordinates are (x, y). Plot the points on the graph and join them.
The graph formed will be a straight line.
Monitoring Progress and Modeling with Mathematics
In Exercises 3–10, tell whether the ordered pair is a solution of the inequality.
Question 3.
x + y < 7; (2, 3)
Answer:
Question 4.
x – y ≤ 0; (5, 2)
Answer:
x – y ≤ 0
5 – 2≤ 0
3 ≤ 0
So, (5, 2) is not a solution to inequality.
Question 5.
x + 3y ≥ -2; (-9, 2)
Answer:
Question 6.
8x + y > -6; (-1, 2)
Answer:
8x + y > -6
8(-1) + 2 > -6
-8 + 2 > -6
-6 > -6
So, (-1, 2) is not a solution to inequality.
Question 7.
-6x + 4y ≤ 6; (-3, -3)
Answer:
Question 8.
3x – 5y ≥ 2; (-1, -1)
Answer:
3x – 5y ≥ 2
3(-1) – 5(-1) ≥ 2
-3 + 5 ≥ 2
2 ≥ 2
So, (-1, -1) is a solution of the inequality.
Question 9.
-x – 6y > 12; (-8, 2)
Answer:
Question 10.
-4x – 8y < 15; (-6, 3)
Answer:
-4x – 8y < 15
-4(-6) – 8(3) < 15
24 – 24 < 15
0 < 15
So, (-6, 3) is a solution of the inequality.
In Exercises 11−16, tell whether the ordered pair is a solution of the inequality whose graph is shown.
Question 11.
(0, -1)
Answer:
Question 12.
(-1, 3)
Answer: Yes, (-1, 3) is a solution because it lies in the shaded half-plane.
Question 13.
(1, 4)
Answer:
Question 14.
(0, 0)
Answer: Yes, (0, 0) is a solution because it lies in the shaded half-plane.
Question 15.
(3, 3)
Answer:
Question 16.
(2, 1)
Answer: No, (2, 1) is not a solution because it lies in the shaded half-plane.
Question 17.
MODELING WITH MATHEMATICS
A carpenter has at most $250 to spend on lumber. The inequality 8x + 12y ≤ 250 represents the numbers x of 2-by-8boards and the numbers y of 4-by-4 boards the carpenter can buy. Can the carpenter buy twelve 2-by-8 boards and fourteen 4-by-4 boards? Explain.
Answer:
Question 18.
MODELING WITH MATHEMATICS
The inequality 3x + 2y ≥ 93 represents the numbers x of multiple- choice questions and the numbers y of matching questions you can answer correctly to receive an A on a test. You answer 20 multiple-choice questions and 18 matching questions correctly. Do you receive an A on the test? Explain.
Answer:
The ordered pair is (20, 18)
3x + 2y ≥ 93
3(20) + 2(18) ≥ 93
60 + 36 ≥ 93
96 ≥ 93
So, the inequality is true.
In Exercises 19–24, graph the inequality in a coordinate plane.
Question 19.
y ≤ 5
Answer:
Question 20.
y > 6
Answer:
Question 21.
x < 2
Answer:
Question 22.
x ≥ -3
Answer:
Question 23.
y > -7
Answer:
Question 24.
x < 9
Answer:
In Exercises 25−30, graph the inequality in a coordinate plane.
Question 25.
y > -2x – 4
Answer:
Question 26.
y ≤ 3x – 1
Answer:
Question 27.
-4x + y < -7
Answer:
Question 28.
3x – y ≥ 5
Answer:
Question 29.
5x – 2y ≤ 6
Answer:
Question 30.
-x + 4y > -12
Answer:
ERROR ANALYSIS In Exercises 31 and 32, describe and correct the error in graphing the inequality.
Question 31.
y < -x + 1
Answer:
Question 32.
y ≤ 3x – 2
Answer:
Question 33.
MODELING WITH MATHEMATICS
You have at most $20 to spend at an arcade. Arcade games cost $0.75 each, and snacks cost $2.25 each. Write and graph an inequality that represents the numbers of games you can play and snacks you can buy. Identify and interpret two solutions of the inequality.
Answer:


Question 34.
MODELING WITH MATHEMATICS
A drama club must sell at least $1500 worth of tickets to cover the expenses of producing a play. Write and graph an inequality that represents how many adult and student tickets the club must sell. Identify and interpret two solutions of the inequality.
Answer:
A drama club must sell at least $1500 worth of tickets to cover the expenses of producing a play.
The tickets sold should be worth greater than or equal to $1500.
Ax + By ≥ 1500
In Exercises 35–38, write an inequality that represents the graph.
Question 35.
Answer:
Question 36.
Answer:
The line passes through (0, 2) and (4, 4)
m = y2-y1/x2-x1
m = 4-2/4-0
m = 2/4
m = 1/2
equation of the line is
y-y1 = m(x-x1)
y – 2 = 1/2(x-0)
y – 2 = 1/2x
2y – 4 = x
x – 2y = 4
(0, 0)
0 – 2(0) < 4
0 < 4
Question 37.
Answer:
Question 38.
Answer:
m = y2-y1/x2-x1
m = 0 + 3/1 – 0
m = 3/1
m = 3
equation of the line is
y-y1 = m(x-x1)
y + 3 = 3(x – 0)
y + 3 = 3x
3x – y = 3
3(0) – 0 ? 3
0 ≥ 3
3x – y ≥ 3
Question 39.
PROBLEM SOLVING
Large boxes weigh 75 pounds, and small boxes weigh 40 pounds.
a. Write and graph an inequality that represents the numbers of large and small boxes a 200-pound delivery person can take on the elevator.
b. Explain why some solutions of the inequality might not be practical in real life.
Answer:


Question 40.
HOW DO YOU SEE IT?
Match each inequality with its graph.
a. 3x – 2y ≤ 6
b. 3x – 2y < 6
c. 3x – 2y > 6
d. 3x – 2y ≥ 6
Answer:
a. 3x – 2y ≤ 6 matches with graph C.
b. 3x – 2y < 6 matches with graph A.
c. 3x – 2y > 6 matches with graph D.
d. 3x – 2y ≥ 6 matches with graph B.
Question 41.
REASONING
When graphing a linear inequality in two variables, why must you choose a test point that is not on the boundary line?
Answer:
You have to know which side of the boundary line to shade. So, you need to choose a point on one side or the other of the boundary line to know which region contains the solutions of the inequality.
Question 42.
THOUGHT PROVOKING
Write a linear inequality in two variables that has the following two properties.
• (0, 0), (0, -1), and (0, 1) are not solutions.
• (1, 1), (3, -1), and (-1, 3) are solutions.
Answer:
(1, 1), (3, -1), and (-1, 3) are solutions.
(0, 0), (0, -1), and (0, 1) are not solutions.
m = y2-y1/x2-x1
m = 1-2/1-0
m = -1/1
m = -1
y = mx + b
y = -1x + 2
y = -x + 2
y ? -x + 2
2 > -2 + 2
2 ≥ 0
So, the inequality is y ≥ -x + 2
Question 43.
WRITING
Can you always use (0, 0) as a test point when graphing an inequality? Explain.
Answer:
CRITICAL THINKING
In Exercises 44 and 45, write and graph an inequality whose graph is described by the given information.
Question 44.
The points (2, 5) and (−3, −5) lie on the boundary line. The points (6, 5) and (−2, −3) are solutions of the inequality.
Answer:
The points (2, 5) and (−3, −5) lie on the boundary line.
The points (6, 5) and (−2, −3) are solutions of the inequality.
Find the equation of the boundary line
Since the boundary line intersect the y-axis at (0, 1)
So, the y-intercept is b = 1.
m = y2-y1/x2-x1
m = -5-5/-3-2
m = 2
y = 2x + 1
Substitute x = 6 and y = 5
5 = 2(6) + 1
5 = 12 + 1
5 ≤ 13
So, y ≤ 2x + 1
Question 45.
The points (−7, −16) and (1, 8) lie on the boundary line. The points (−7, 0) and (3, 14) are not solutions of the inequality.
Answer:

Maintaining Mathematical Proficiency
Write the next three terms of the arithmetic sequence.
Question 46.
0, 8, 16, 24, 32, . . .
Answer:
0, 8, 16, 24, 32, . . .
a1 = 0 and the second term a2 = 8
d = a1 – a2
= 8 – 0
= 8
an = a + (n – 1)d
a6 = a + (6 – 1)d
= a + 5d
= 0 + 5(8)
= 0 + 40
a7 = a + (7 – 1)d
= a + 6d
= 0 + 6(8)
= 48
a8 = a + (8 – 1)d
= a + 7d
= 0 + 7(8)
= 0 + 56
= 56
The next three terms in the arithmetic sequence are 40, 48, 56.
Question 47.
-5, -8, -11, -14, -17, . . .
Answer:
Question 48.
\(-\frac{3}{2},-\frac{1}{2}, \frac{1}{2}, \frac{3}{2}, \frac{5}{2}, \ldots\)
Answer:
a1 = -3/2
a2 = -1/2
d = -1/2 – (-3/2)
d = 1
a6 = 5/2 + 1
= 7/2
a7 = a6 + d
= 7/2 + 1
= 9/2
a8 = 9/2 + 1
= 11/2
So, the next three terms are 7/2, 9/2, 11/2
Lesson 5.7 Systems of Linear Inequalities
Essential Question How can you graph a system of linear inequalities?
EXPLORATION 1
Graphing Linear Inequalities
Work with a partner. Match each linear inequality with its graph. Explain your reasoning.
2x + y ≤ 4 Inequality 1
2x – y ≤ 0 Inequality 2
Answer:
Equality of the first inequality 2x + y ≤ 4 i.e, 2x + y = 4
The line passes through the points (2, 0) and (0, 4).
So, the first inequality will be matched with the graph A.
Equality of the second inequality 2x – y ≤ 0 Inequality 2
The line passes through (0, 0)
So, the second inequality will be matched with the graph B.
EXPLORATION 2
Graphing a System of Linear Inequalities
Work with a partner. Consider the linear inequalities given in Exploration 1.
2x + y ≤ 4 Inequality 1
2x – y ≤ 0 Inequality 2
a. Use two different colors to graph the inequalities in the same coordinate plane. What is the result?
b. Describe each of the shaded regions of the graph. What does the unshaded region represent?
Communicate Your Answer

Question 3.
How can you graph a system of linear inequalities?
Answer:
Graph the line using the slope and y-intercept. If the sign is greater/less than or equal to, the line will be solid (to include the points on the line). If it is just greater or less than, the line will be dashed. If the sign is < the part of the graph that contains data points less than the line will be shaded. If the sign is > shade the part of the graph that has the points greater than the line.
Question 4.
When graphing a system of linear inequalities, which region represents the solution of the system?
Answer: The inequality sign indicates the region that is part of the solution.
Question 5.
Do you think all systems of linear inequalities have a solution? Explain your reasoning.
Answer:
Let the equations be
x > 2
x < 1
There is no common shaded region.
So, there will be bo solution for the linear inequalities.
Question 6.
Write a system of linear inequalities represented by the graph.
Answer:
Let the line passes through the points (0, 2) and (1, -1)
y – y1 = y2-y1/x2-x1(x-x1)
y – 2 = -1-2/1-0(x-0)
y – 2 = -3x
y = -3x + 2
y ≥ -3x + 2
Let the line passes through the points (0, -2) and (3, 0)
y – (-2) = 0 – (-2)/3-0(x- 0)
y + 2 = 2/3x
y = 2/3x – 2
y ≥ 2/3x – 2
Monitoring Progress
Tell whether the ordered pair is a solution of the system of linear inequalities.
Question 1.
(-1, 5); y < 5 y > x – 4
Answer:
y < 5
(-1, 5)
5 < 5
(-1, 5) is the solution of the system of linear inequalities.
y > x – 4
5 > -1 – 4
5 > -5
(-1, 5) is the solution of the system of linear inequalities.
Question 2.
(1, 4); y ≥ 3x + 1
y > x – 1
Answer:
y ≥ 3x + 1
(1, 4)
4 ≥ 3(1) + 1
4 ≥ 4
(1, 4) is the solution of the system of linear inequalities.
y > x – 1
4 > 1 – 1
4 > 0
(1, 4) is the solution of the system of linear inequalities.
Graph the system of linear inequalities.
Question 3.
y ≥ -x + 4
x + y ≤ 0
Answer:
Question 4.
y > 2x – 3
y ≥ \(\frac{1}{2}\)x + 1
Answer:
Question 5.
-2x + y < 4 2x + y > 4
Answer:
Write a system of linear inequalities represented by the graph.
Question 6.
Answer:
Question 7.
Answer:
Question 8.
Name another solution of Example 6.
Answer:
Question 9.
WHAT IF?
You want to spend at least 3 hours at the mall. How does this change the system? Is (2.5, 5) still a solution? Explain.
Answer:
Given,
You want to spend at least 3 hours at the mall.
Number of hours at the mall = x
Number of hours in beach = y
x + y ≤ 8 at most 8 hours at the hall
x ≥ 3 at least 3 hours at the mall
y > 4 more than 4 hours at the beach
The solution region of the linear system is (3, 5).
Systems of Linear Inequalities 5.7 Exercises
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
How can you verify that an ordered pair is a solution of a system of linear inequalities?
Answer: You can substitute the values into each inequality of the system and verify that the values make the inequalities true.
Question 2.
WHICH ONE DOESN’T BELONG?
Use the graph shown. Which of the ordered pairs does not belong with the other three? Explain your reasoning.
Answer:
From the graph the shaded region represents the solution of the system of inequalities.
Since the ordered pairs (0, -4) and (-1, -6) lies in the shaded region.
Thus (0, -4) and (-1, -6) are solutions of the system of inequalities.
Since the ordered pairs (2, -4) lies on the solid line.
Therefore (2, -4) is a solution of the system of inequalities.
Since the ordered pair (1, -2) lies on the dashed line.
Thus (1, -2) is not a solution of the system of the inequalities.
Therefore, (1, -2) does not belong with the other three.
Monitoring Progress and Modeling with Mathematics
In Exercises 3−6, tell whether the ordered pair is a solution of the system of linear inequalities.
Question 3.
(-4, 3)
Answer:
Question 4.
(-3, -1)
Answer: Yes, the ordered pair (-3, -1) is the solution of one inequality. It is in the shaded region.
Question 5.
(-2, 5)
Answer:
Question 6.
(1, 1)
Answer: No, the ordered pair (1, 1) is not in the shaded region. So, it is not the solution of the system.
In Exercises 7−10, tell whether the ordered pair is a solution of the system of linear inequalities.
Question 7.
(-5, 2); y < 4
y > x + 3
Answer:
Question 8.
(1, -1); y > -2
y > x – 5
Answer:
y > -2
-1 > -2
y > x – 5
-1 > 1 – 5
-1 > -4
Because the ordered pair (1, -1) is a solution of each inequality, it is a solution of the system.
Question 9.
(0, 0); y ≤ x + 7
y ≥ 2x + 3
Answer:
Question 10.
(4, -3); y ≤ -x + 1
y ≤ 5x – 2
Answer:
y ≤ -x + 1
-3 ≤ -4 + 1
-3 ≤ -3
y ≤ 5x – 2
-3 ≤ 5(4) – 2
-3 ≤ 20 – 2
-3 ≤ 18
In Exercises 11−20, graph the system of linear inequalities.
Question 11.
y > -3
y ≥ 5x
Answer:
Question 12.
y < -1
x > 4
Answer:
Question 13.
y < -2 y > 2
Answer:
Question 14.
y < x – 1
y ≥ x + 1
Answer:
Question 15.
y ≥ -5
y – 1 < 3x Answer: Question 16. x + y > 4
y ≥ \(\frac{3}{2}\)x – 9
Answer:
Question 17.
x + y > 1
-x – y < -3
Answer:
Question 18.
2x + y ≤ 5
y + 2 ≥ -2x
Answer:
Question 19.
x < 4
y > 1
y ≥ -x + 1
Answer:
Question 20.
x + y ≤ 10
x – y ≥ 2
y > 2
Answer:
In Exercises 21−26, write a system of linear inequalities represented by the graph.
Question 21.
Answer:
Question 22.
Answer:
Inequality 1: The line passes through the point (2, 0)
Inequality 2: The line passes through the points (4, 0)
The system of linear inequalities represented by the graph is x < 4 and x > 2.
Question 23.
Answer:
Question 24.
Answer:
The line passes through the points (0, 1) and (-1, 4)
m = 4-1/-1-0
= 3/-1
= -3
The y-intercept of the line is 1.
Substitute -3 for m and 1 for c in the equation of line y = mx + c
y = mx + c
y = -3x + 1
The shaded region is to the right side of the line.
y ≥ -3x + 1.
The second line passes through the points (2, 0) and (0, -2)
m = -2-0/0-2
m = -2/-2
m = 1
y = mx + c
y = x – 2
y > x – 2
Question 25.
Answer:
Question 26.
Answer:
The boundary line intersects the y-axis at (0, 0).
b = 0
The line passes through the points (0, 0) and (3, 1)
m = y2-y1/x2-x1
m = 1-0/3-0
m = 1/3
y = 1/3x
Here the shaded region have the points (1, 1)
1 > 1/3 . 1
1 ≥ 1/3
y ≥ 1/3 x
The boundary line intersects the y-axis at (0, -2).
b = -2
The line passes through the points (0, -2) and (3, -1)
m = y2-y1/x2-x1
m = -1-(-2)/3-0
m = 1/3
y = 1/3x – 2
1 ? 1/3 . 1 – 2
1 ≥ -5/3
y ≥ 1/3x – 2
ERROR ANALYSIS In Exercises 27 and 28, describe and correct the error in graphing the system of linear inequalities.
Question 27.
Answer:
Question 28.
Answer:
Question 29.
MODELING WITH MATHEMATICS
You can spend at most $21 on fruit. Blueberries cost $4 per pound, and strawberries cost $3 per pound. You need at least 3 pounds of fruit to make muffins.
a. Write and graph a system of linear inequalities that represents the situation.
b. Identify and interpret a solution of the system.
c. Use the graph to determine whether you can buy 4 pounds of blueberries and 1 pound of strawberries.
Answer:


Question 30.
MODELING WITH MATHEMATICS
You earn $10 per hour working as a manager at a grocery store. You are required to work at the grocery store at least 8 hours per week. You also teach music lessons for $15 per hour. You need to earn at least $120 per week, but you do not want to work more than 20 hours per week.
a. Write and graph a system of linear inequalities that represents the situation.
b. Identify and interpret a solution of the system.
c. Use the graph to determine whether you can work 8 hours at the grocery store and teach 1 hour of music lessons.
Answer:
Given,
You earn $10 per hour working as a manager at a grocery store.
Earning for x hours = 10x
You are required to work at the grocery store at least 8 hours per week.
You also teach music lessons for $15 per hour.
For y hours = 15y
You need to earn at least $120 per week, but you do not want to work more than 20 hours per week.
x + y ≤ 20
Total earning = 10x + 15y
10x + 15y ≥ 120
x ≥ 8
Question 31.
MODELING WITH MATHEMATICS
You are fishing for surfperch and rockfish, which are species of bottomfish. Gaming laws allow you to catch no more than 15 surfperch per day, no more than 10 rockfish per day, and no more than 20 total bottomfish per day.
a. Write and graph a system of linear inequalities that represents the situation.
b. Use the graph to determine whether you can catch 11 surfperch and 9 rockfish in 1 day.
Answer:

Question 32.
REASONING
Describe the intersection of the half-planes of the system shown.
x – y ≤ 4
x – y ≥ 4
Answer:
Question 33.
MATHEMATICAL CONNECTIONS
The following points are the vertices of a shaded rectangle.
(-1, 1), (6, 1), (6, -3), (-1, -3)
a. Write a system of linear inequalities represented by the shaded rectangle.
b. Find the area of the rectangle.
Answer:
Question 34.
MATHEMATICAL CONNECTIONS
The following points are the vertices of a shaded triangle.
(2, 5), (6, -3), (-2, -3)
a. Write a system of linear inequalities represented by the shaded triangle.
b. Find the area of the triangle.
Answer:
a. (2, 5), (6, -3), (-2, -3)
For (-2, -3) & (2, 5), y = 2x + 1
For (6, -3) & (2, 5), y = -2x + 9
For (-2, -3) & (6, -3), y = -3
The system of a linear inequality is
y ≤ 2x + 1
y ≤ -2x + 9
y ≥ -3
b. A = 1/2 bh
A = 1/2 (8) (8)
A = 32 square units
The area of the triangle is 32 sq. units.
Question 35.
PROBLEM SOLVING
You plan to spend less than half of your monthly $2000 paycheck on housing and savings. You want to spend at least 10% of your paycheck on savings and at most 30% of it on housing. How much money can you spend on savings and housing?
Answer:

Question 36.
PROBLEM SOLVING
On a road trip with a friend, you drive about 70 miles per hour, and your friend drives about 60 miles per hour. The plan is to drive less than 15 hours and at least 600 miles each day. Your friend will drive more hours than you. How many hours can you and your friend each drive in 1 day?
Answer:
Given,
On a road trip with a friend, you drive about 70 miles per hour, and your friend drives about 60 miles per hour.
The plan is to drive less than 15 hours
x + y < 15
and at least 600 miles each day.
70x + 60y ≥ 600
A = (0, 15), B = (0, 10), C = (8.571, 0), D = (10, 0)
x = 0, y = 10
Distance = 70 × 0 + 60 × 10
= 600
600 ≥ 600 and x + y = 0 + 0 < 15
We drive for 0 hours and our friend drives 10 hours.
Question 37.
WRITING
How are solving systems of linear inequalities and solving systems of linear equations similar? How are they different?
Answer:
Question 38.
HOW DO YOU SEE IT?
The graphs of two linear equations are shown.
Replace the equal signs with inequality symbols to create a system of linear inequalities that has point C as a solution, but not points A, B, and D. Explain your reasoning.
Answer:
The line y = -3x + 4 must have the shaded region above it and since B is not a solution, then the boundary line is dashed y > -3x + 4
The line y = 2x + 1 must have the shaded region below it and since there are no points on this boundary line, y ≤ 2x + 1.
Question 39.
USING STRUCTURE
Write a system of linear inequalities that is equivalent to |y| < x, where x > 0. Graph the system.
Answer:
Question 40.
MAKING AN ARGUMENT
Your friend says that a system of linear inequalities in which the boundary lines are parallel must have no solution. Is your friend correct? Explain.
Answer: No, our friend’s statement is incorrect, because a system of linear inequalities in which the boundary lines are parallel has the solution region sometimes.
Example:
Question 41.
CRITICAL THINKING
Is it possible for the solution set of a system of linear inequalities to be all real numbers? Explain your reasoning.
Answer:
OPEN-ENDED In Exercises 42−44, write a system of linear inequalities with the given characteristic.
Question 42.
All solutions are in Quadrant I.
Answer: If all solutions are points in Quadrant -1 then the x-coordinates and y-coordinates of all those points are all positive.
Question 43.
All solutions have one positive coordinate and one negative coordinate.
Answer:
Question 44.
There are no solutions.
Answer:
y > x + 2
y < x – 2
There are no solutions
Question 45.
OPEN-ENDED
One inequality in a system is -4x + 2y > 6. Write another inequality so the system has (a) no solution and (b) infinitely many solutions.
Answer:
Question 46.
THOUGHT PROVOKING
You receive a gift certificate for a clothing store and plan to use it to buy T-shirts and sweatshirts. Describe a situation in which you can buy 9 T-shirts and 1 sweatshirt, but you cannot buy 3 T-shirts and 8 sweatshirts. Write and graph a system of linear inequalities that represents the situation.
Answer:
Question 47.
CRITICAL THINKING
Write a system of linear inequalities that has exactly one solution.
Answer:
Question 48.
MODELING WITH MATHEMATICS
You make necklaces and key chains to sell at a craft fair. The table shows the amounts of time and money it takes to make a necklace and a key chain, and the amounts of time and money you have available for making them.
a. Write and graph a system of four linear inequalities that represents the number x of necklaces and the number y of key chains that you can make.
b. Find the vertices (corner points) of the graph of the system.
c. You sell each necklace for $10 and each key chain for $8. The revenue R is given by the equation R = 10x + 8y. Find the revenue corresponding to each ordered pair in part (b). Which vertex results in the maximum revenue?
Answer:
a.
Let x be the number of necklaces and y be the number of key chains.
x ≥ 0
y ≥ 0
0.5x + 0.25y ≤ 20
2x + 3y ≤ 120
b.
y = 20 – 0.5x/0.25
y = (120 – 2x)/3
c.
The values at P1
R(x, y) = R(0, 0)
R(0, 0) = 10 × 0 + 8 × 0
= 0
at P2
R(x, y) = R(0, 60)
R(0, 60) = 10 × 0 + 8 × 60
= 480
at P3
R(x, y) = R(0, 0)
R(40, 0) = 10 × 40 + 8 × 0
= 400
at P4
R(x, y) = R(0, 0)
R(30, 20) = 10 × 30 + 8 × 20
= 460
The maximal value of the revenue function is at P2, and it gives the optimal solution for the revenue.
The maximum revenue is $480 and it is achieved at 0 necklaces and 60 keychains.
Maintaining Mathematical Proficiency
Write the product using exponents.
Question 49.
4 • 4 • 4 • 4 • 4
Answer:
4 • 4 • 4 • 4 • 4 = 45
Question 50.
(-13) • (-13) • (-13)
Answer:
(-13) • (-13) • (-13) = (-13)³
Question 51.
x • x • x • x • x • x
Answer:
x • x • x • x • x • x = x6
Write an equation of the line with the given slope and y-intercept.
Question 52.
slope: 1
y-intercept: -6
Answer:
Equation of the line is y = mx + b
m = 1
b = -6
y = (1)x + (-6)
y = x – 6
Question 53.
slope: -3
y-intercept: 5
Answer:
Question 54.
slope: –\(\frac{1}{4}\)
y-intercept: -1
Answer:
Equation of the line is y = mx + b
m = –\(\frac{1}{4}\)
b = -1
y = –\(\frac{1}{4}\)x + (-1)
y = –\(\frac{1}{4}\)x – 1
Question 55.
slope: \(\frac{4}{3}\)
y-intercept: 0
Answer:
Solving Systems of Linear Equations Performance Task: Prize Patrol
5.5–5.7 What Did You Learn?
Core Vocabulary
Core Concepts
Section 5.5
Solving Linear Equations by Graphing, p. 262
Solving Absolute Value Equations by Graphing, p. 263
Section 5.6
Graphing a Linear Inequality in Two Variables, p. 269
Section 5.7
Graphing a System of Linear Inequalities, p. 275
Writing a System of Linear Inequalities, p. 276
Mathematical Practices
Question 1.
Why do the equations in Exercise 35 on page 266 contain absolute value expressions?
Answer:
Question 2.
Why is it important to be precise when answering part (a) of Exercise 39 on page 272?
Answer:
Question 3.
Describe the overall step-by-step process you used to solve Exercise 35 on page 279.
Answer:
Performance Task Prize Patrol
You have been selected to drive a prize patrol cart and place prizes on the competing teams’ predetermined paths. You know the teams’ routes and you can only make one pass. Where will you place the prizes so that each team will have a chance to find a prize on their route?
To explore the answers to these questions and more, go to
Solving Systems of Linear Equations Chapter Review
5.1 Solving Systems of Linear Equations by Graphing (pp. 235–240)
Solve the system of linear equations by graphing.
Question 1.
y = -3x + 1
y = x – 7
Answer:
Given equations
y = -3x + 1
y = x – 7
Question 2.
y = -4x + 3
4x – 2y = 6
Answer:
Given equations are
y = -4x + 3
4x – 2y = 6
Question 3.
5x + 5y = 15
2x – 2y = 10
Answer:
Given equations
5x + 5y = 15
2x – 2y = 10
5.2 Solving Systems of Linear Equations by Substitution (pp. 241–246)
Solve the system of linear equations by substitution. Check your solution.
Question 4.
3x + y = -9
y = 5x + 7
Answer:
Given equations
3x + y = -9
y = 5x + 7
3x + y = -9
-5x + y = 7
8x = -16
x = -16/8
x = -2
3x + y = -9
3(-2) + y = -9
-6 + y = -9
y = -9 + 6
y = -3
3x + y = -9
3(-2) + (-3) = -9
-6 – 3 = -9
-9 = -9
LHS = RHS
Question 5.
x + 4y = 6
x – y = 1
Answer:
x + 4y = 6
x – y = 1
5y = 5
y = 1
x – y = 1
x – 1 = 1
x = 1 + 1
x = 2
x – y = 1
2 – 1 = 1
1 = 1
Question 6.
2x + 3y = 4
y + 3x = 6
Answer:
2x + 3y = 4
y + 3x = 6
2x + 3y = 4
y + 3x = 6 —- × 3 ⇒ 3y + 9x = 18
2x + 3y = 4
9x + 3y = 18
-7x = -14
x = 2
2x + 3y = 4
2(2) + 3y = 4
4 + 3y = 4
3y = 0
y = 0
2x + 3y = 4
2(2) + 3(0) = 4
4 + 0 = 4
4 = 4
LHS = RHS
Question 7.
You spend $20 total on tubes of paint and disposable brushes for an art project. Tubes of paint cost $4.00 each and paintbrushes cost $0.50 each. You purchase twice as many brushes as tubes of paint. How many brushes and tubes of paint do you purchase?
Answer:
Given,
You spend $20 total on tubes of paint and disposable brushes for an art project.
Tubes of paint cost $4.00 each and paintbrushes cost $0.50 each.
Let x be the total number of paint tubes
y be the number of paintbrushes
4x + 0.5y = 20
y = 2x
4x + 0.5(2x) = 20
5x = 20
x = 4
4x + 0.5y = 20
4(4) + 0.5y = 20
16 + 0.5y = 20
0.5y = 4
y = 8
The number of paintbrushes purchased is 4 and the number of tubes of paint purchased is 8.
5.3 Solving Systems of Linear Equations by Elimination (pp. 247 – 252)
Solve the system of linear equations by elimination. Check your solution.
Question 8.
9x – 2y = 34
5x + 2y = -6
Answer:
9x – 2y = 34
5x + 2y = -6
14x = 28
x = 28/14
x = 2
5x + 2y = -6
5(2) + 2y = -6
10 + 2y = -6
2y = -6 – 10
2y = -16
y = -8
Check:
5x + 2y = -6
5(2) + 2(-8) = -6
10 – 16 = -6
-6 = -6
LHS = RHS
Question 9.
x + 6y = 28
2x – 3y = -19
Answer:
x + 6y = 28
2x – 3y = -19 — × 2
x + 6y = 28
4x – 6y = -38
5x = -10
x = -2
-2 + 6y = 28
6y = 28 + 2
6y = 30
y = 5
Check:
x + 6y = 28
-2 + 6(5) = 28
-2 + 30 = 28
28 = 28
LHS = RHS
Question 10.
8x – 7y = -3
6x – 5y = -1
Answer:
8x – 7y = -3 —- × 5 ⇒ 40x – 35y = -15
6x – 5y = -1 —- × 7 ⇒ 42x – 35y = -4
40x – 35y = -15
42x – 35y = -4
-2x = 11
x = -11/2
6x – 5y = -1
6(-11/2) – 5y = -1
3(-11) -5y = -1
-33 – 5y = -1
-5y = -1 + 33
-5y = 32
y = -32/5
5.4 Solving Special Systems of Linear Equations (pp. 253–258)
Solve the system of linear equations.
Question 11.
x = y + 2
-3x + 3y = 6
Answer:
x = y + 2 ⇒ x – y = 2
-3x + 3y = 6 ⇒ -x + y = 2
x – y = 2
-x + y = 2
0 = 2
LHS ≠ RHS
Question 12.
3x – 6y = -9
-5x + 10y = 10
Answer:
3x – 6y = -9 ⇒ x – 2y = -3
-5x + 10y = 10 ⇒ -x + 2y = 2
x – 2y = -3
-x + 2y = 2
0 = -1
LHS ≠ RHS
Question 13.
-4x + 4y = 32
3x + 24 = 3y
Answer:
-4x + 4y = 32 ⇒ -x + y = 8
3x + 24 = 3y ⇒ x -y = – 8
-x + y = 8
x -y = – 8
0 = 0
LHS = RHS
5.5 Solving Equations by Graphing (pp. 261–26
Solve the equation by graphing. Check your solution(s).
Question 14.
\(\frac{1}{3}\)x + 5 = -2x – 2
Answer:
\(\frac{1}{3}\)x + 5 = -2x – 2
\(\frac{1}{3}\)x + 2x = -2 – 5
\(\frac{7}{3}\)x = -7
7x = -21
x = -21/7
x = -3
Question 15.
|x + 1| = |-x – 9|
Answer:
|x + 1| = |-x – 9|
x + 1 = -x – 9
2x = -9 – 1
2x = -10
x = -5
Question 16.
|2x – 8| = |x + 5|
Answer:
|2x – 8| = |x + 5|
2x – 8 = x + 5
2x – x = 5 + 8
x = 13
5.6 Graphing Linear Inequalities in Two Variables (pp. 267–272)
Graph the inequality in a coordinate plane.
Question 17.
y > -4
Answer:
Question 18.
-9x + 3y ≥ 3
Answer:
-9x + 3y ≥ 3
-3x + y ≥ 1
Question 19.
5x + 10y < 40
Answer:
5x + 10y < 40 ⇒ x + 2y < 8
5.7 Systems of Linear Inequalities (pp. 273–280) Graph the system of linear inequalities.
Question 20.
y ≤ x – 3
y ≥ x + 1
Answer:
y ≤ x – 3
y ≥ x + 1
Question 21.
y > -2x + 3
y ≥ \(\frac{1}{4}\)x – 1
Answer:
y > -2x + 3
y ≥ \(\frac{1}{4}\)x – 1
Question 22.
x + 3y > 6
2x + y < 7
Answer:
Solving Systems of Linear Equations Chapter Test
Solve the system of linear equations using any method. Explain why you chose the method.
Question 1.
8x + 3y = -9
-8x + y = 29
Answer:
8x + 3y = -9
-8x + y = 29
2y = 20
y = 20/2
y = 10
-8x + y = 29
-8x + 10 = 29
-8x = 19
x = -19/8
Question 2.
\(\frac{1}{2}\)x + y = -6
y = \(\frac{3}{5}\)x + 5
Answer:
\(\frac{1}{2}\)x + y = -6
y = \(\frac{3}{5}\)x + 5
\(\frac{1}{2}\)x + y = -6
\(\frac{3}{5}\)x – y = -5
\(\frac{1}{2}\)x + \(\frac{3}{5}\)x = -11
5x + 15x = -110
x + 3x = -22
4x = -22
x = -11/2
y = \(\frac{3}{5}\)x + 5
y = \(\frac{3}{5}\)(-11/2) + 5
y = \(\frac{-33}{10}\) + 5
y = -3.3 + 5
y = 1.7
Question 3.
y = 4x + 4
-8x + 2y = 8
Answer:
y = 4x + 4
-8x + 2y = 8 ⇒ -4x + y = 4
4x – y = -4
-4x + y = 4
0 = 0
Question 4.
x = y – 11
x – 3y = 1
Answer:
x = y – 11 ⇒ x – y = -11
x – 3y = 1
x – y = -11
x – 3y = 1
2y = -12
y = -6
x – y = -11
x + 6 = -11
x = -11 – 6
x = -17
Question 5.
6x – 4y = 9
9x – 6y = 15
Answer:
6x – 4y = 9
9x – 6y = 15 ⇒ 3x – 2y = 5— × 2
6x – 4y = 9
6x – 4y = 10
0 = -1
LHS ≠ RHS
Question 6.
y = 5x – 7
-4x + y = -1
Answer:
y = 5x – 7 ⇒ 5x – y = 7
-4x + y = -1 ⇒ -4x + y = -1
5x – y = 7
-4x + y = -1
x = 6
5(6) – y = 7
30 – y = 7
30 – 7 = y
y = 23
Question 7.
Write a system of linear inequalities so the points (1, 2) and (4, -3) are solutions of the system, but the point (-2, 8) is not a solution of the system.
Answer:
(1, 2) and (4, -3)
m = -3-2/(4-1)
m = -5/3
y – y1 = m(x – x1)
y – 2 = -5/3(x – 1)
y – 2 = -5/3x + 5/3
y = -5/3x + 11/3
y = -5/3(-2) + 11/3
8 > 1/3
y ≤ -5/3x + 11/3
Question 8.
How is solving the equation |2x + 1| = |x – 7| by graphing similar to solving the equation 4x + 3 = -2x + 9 by graphing? How is it different?
Answer:
|2x + 1| = |x – 7|
2x + 1 = x – 7
2x – x = -7 – 1
x = -8
4x + 3 = -2x + 9
4x + 2x = 9 – 3
6x = 6
x = 1
Graph the system of linear inequalities.
Question 9.
y > \(\frac{1}{2}\)x + 4
2y ≤ x + 4
Answer:
Question 10.
x + y < 1
5x + y > 4
Answer:
x + y < 1
5x + y > 4
Question 11.
y ≥ – \(\frac{2}{3}\)x + 1
-3x + y > -2
Answer:
Question 12.
You pay $45.50 for 10 gallons of gasoline and 2 quarts of oil at a gas station. Your friend pays $22.75 for 5 gallons of the same gasoline and 1 quart of the same oil.
a. Is there enough information to determine the cost of 1 gallon of gasoline and 1 quart of oil? Explain.
b. The receipt shown is for buying the same gasoline and same oil. Is there now enough information to determine the cost of 1 gallon of gasoline and 1 quart of oil? Explain.
c. Determine the cost of 1 gallon of gasoline and 1 quart of oil.
Answer:
a. You pay $45.50 for 10 gallons of gasoline and 2 quarts of oil at a gas station.
10x + 2y = 45.50 — eq(1)
Your friend pays $22.75 for 5 gallons of the same gasoline and 1 quart of the same oil.
5x + y = 22.75 — eq(2)
2(5x + y) = 2 × 22.75
10x + 2y = 45.50
10x + 2y – 10x – 2y = 45.50 – 45.50
0 = 0
b. Let x be the cost of 1 gallon of gasoline and y be the cost of 1 quarts of oil
8x + 2y = 38.40
10x + 2y = 45.50
Thus there is not enough information to determine the cost of 1 gallon of gasoline and 1 quart of oil.
c. 10x + 2y = 45.50
8x + 2y = 38.40
Solve both equations
10x + 2y – (8x + 2y) = 45.50 – 38.40
10x + 2y – 8x – 2y = 7.1
2x = 7.1
x = 3.55
10 × 3.55 + 2y = 45.50
35.50 + 2y = 45.50
2y = 45.50 – 35.50
2y = 10
y = 5
Question 13.
Describe the advantages and disadvantages of solving a system of linear equations by graphing.
Answer:
Advantages:
1. We can determine the solutions easily from the graph.
2. It is easy to graph the equation by writing it in intercept form.
Disadvantages:
1. The graph is difficult to draw if we are dealing with equations having radicals.
Question 14.
You have at most $60 to spend on trophies and medals to give as prizes for a contest.
a. Write and graph an inequality that represents the numbers of trophies and medals you can buy. Identify and interpret a solution of the inequality.
b. You want to purchase at least 6 items. Write and graph a system that represents the situation. How many of each item can you buy?
Answer:
You have at most $60 to spend on trophies and medals to give as prizes for a contest.
12x + 3y ≤ 60
4x + y ≤ 20
Slope is -4 and y-intercept is 20.
12(0) + 3(0) ≤ 60
0 ≤ 60
(0, 0) is the solution of the inequality.
Any point lies in the shaded region is a solution of the inequality, thus the point (2, 6) is a possible solution.
It means you can buy 2 trophies and 6 medals.
put x = 4 and y = 4
12x + 3y
12(4) + 3(4)
48 + 12 = 60
60 = 60
Question 15.
Compare the slopes and y-intercepts of the graphs of the equations in the linear system 8x + 4y = 12 and 3y = -6x – 15 to determine whether the system has one solution, no solution, or infinitely many solutions. Explain.
Answer:
8x + 4y = 12 and
3y = -6x – 15
y = -2x + 3
3y = -6x – 15
y = -2x – 5
So, both equations have a slope of -2.
But one has a y-intercept of 3 and the other has a y-intercept of -5.
They are parallel so they will never intersect.
So, the system has no solutions.
Solving Systems of Linear Equations Cumulative Assessment
Question 1.
The graph of which equation is shown?
Answer:
Use a graphing calculator to find the equation.
-9x + 2y = -18 matches the graph.
Option D is the correct answer.
Question 2.
A van rental company rents out 6-, 8-, 12-, and 16-passenger vans. The function C(x) = 100 + 5x represents the cost C (in dollars) of renting an x-passenger van for a day. Choose the numbers that are in the range of the function.
Answer:
C(x) = 100 + 5x
Range of the function
x = 6
C(6) = 100 + 5(6) = 100 + 30 = 130
x = 8
C(8) = 100 + 5(8) = 100 + 40 = 140
x = 12
C(6) = 100 + 5(12) = 100 + 60 = 160
x = 16
C(16) = 100 + 5(16) = 100 + 80 = 180
Thus the numbers that are in the range of the function are 130, 140, 160 and 180.
Question 3.
Fill in the system of linear inequalities with <, ≤, >, or ≥ so that the graph represents the system.
Answer:
y≤ 3x -2
y > -x + 5 represents the system.
Question 4.
Your friend claims to be able to fill in each box with a constant so that when you set each side of the equation equal to y and graph the resulting equations, the lines will intersect exactly once. Do you support your friend’s claim? Explain.
Answer:
4x + 4 = 4x + 4 will intersect exactly once.
Question 5.
Select the phrases you should use when describing the transformations from the graph of f to the graph of g.
Answer:
Reflection in the x-axis
vertical stretch
vertical translation
Question 6.
Which two equations form a system of linear equations that has no solution?
Answer:
The equations y = 3x + 2 and y = 3x + 1/2 are parallel.
So, it has no solution.
Question 7.
Fill in a value for a so that each statement is true for the equation ax – 8 = 4 – x.
Answer:
ax – 8 = 4 – x
x = -2
a(-2) – 8= 4 – (-2)
-2a – 8 = 6
-2a = 14
a = -7
a. when a = -7, the solution is x = -2
b. ax – 8 = 4 – x
x = 12
a(12) – 8= 4 – (12)
12a – 8 = -8
12a = 0
a = 0
b. when a = 0, the solution is x = 12
c. ax – 8 = 4 – x
x = 3
a(3) – 8= 4 – (3)
3a – 8 = -1
-2a = 7
a = -7/2
Question 8.
Which ordered pair is a solution of the linear inequality whose graph is shown?
Answer: (-1, -1) is a solution of the linear inequality
Option C is the correct answer.
Question 9.
Which of the systems of linear equations are equivalent?
Answer:
Question 10.
The value of x is more than 9. Which of the inequalities correctly describe the triangle? The perimeter (in feet) is represented by P, and the area (in square feet) is represented by A.
Answer:
Let x = 10
10 + 16 + 13 = 38
So, P > 38
A > 117
